`Всеукраїнський центр проведення олімпіад в мережі Інтернет
  1. Завдання 3-го туру NetOI-2008
З Новим Роком!
        
Розв'язки третього туру приймаються  до 0 годин 21 січня 2008 р.
Задача NewCalc 
Нещодавно Петрик придбав калькулятор фірми NetOI з індикатором на рідких кристалах (інженери фірми NetOI вкрали схему цього калькулятора у фірми NEERC, але потім дещо вдосконалили). Вдосконалений калькулятор може працювати в системах числення з будь-якою основою від 2 до 16 (встановлюється спеціальним перемикачем). Індикатор калькулятора відображає кожну з n цифр за допомогою елементу, що містить сім смужок, кожна з яких може бути або білою, або чорною. Зокрема, при відображенні цифри «1» чорними є дві вертикальні праві смужки. Зображення цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, b, C, d, E та F мають вигляд:

Петрику цікаво, яке максимальне й яке мінімальне натуральне n-значне число в p-ій системі числення можуть бути відображені на індикаторі його нового калькулятора так, щоб чорними були рівно k смужок.Напишіть програму, яка знайде відповідь на Петрикове питання. Враховуйте при цьому, що числа не можуть починатися з нулів.
Технічні умови Програма NewCalc  має прочитати з клавіатури в одному рядку через пропуски (пробіли) три цілі числа: n, k та p (1≤n≤1000, n≤k≤10000, 2≤p≤16) — кількість цифр, кількість чорних смужок та основу системи числення. Програма має вивести на екран в один рядок шукані мінімальне та максимальне число (розділені одним пропуском). Виводити слід саме такі цифри, які використовує калькулятор (зокрема, цифри зі значеннями 11 та 13 — маленькі латинські літери b та d, цифри зі значеннями 10, 12, 14 та 15 — великі літери A, C, E та F). Якщо вказаним чином не можна подати жодне натуральне число, слід вивести єдиний рядок NO SOLUTION.
Приклади
Введення1:             5 15 10
Виведення1:           10117 97111
Введення2:            1 3 2
Виведення2           NO SOLUTION
Введення3:             1 4 15
Виведення3:           4 C

Задача LampsPlus

 
Дано 2n лампочок, кожна з яких може бути в стані «вкл» та «викл». Спочатку всі лампочки в стані «викл». Якась лампочка  змінює свій стан на протилежний, так повторюється k разів (k-n – парне число), в результаті лампочки 1..n знаходяться в стані «вкл», а лампочки n+1..2n –«викл». Хай  P – кількість таких послідовностей перемикань, а L кількість таких послідовностей, в яких  стан лампочок n+1..2n  не змінювався жодного разу. Знайти P та L 
Технічні умови. Програма   LampsPlus читає з клавіатури 2 натуральних  числа n та k (n<=50, k<=100) в одному рядку і виводить одним рядком через пропуск числа L та P
Приклад Введення 2 4
Виведення 8 32

 

Задача Tetris


Ігрове поле для гри Tetris має розміри 4*N  клітинок.  Пластинки, якими воно покривається лише одного виду – такі, як зображено на малюнку. Скільки існує різних способів покриття ігрового поля такими пластинками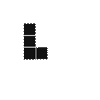

Технічні умови. Програма Tetris читає з клавіатури одне  натуральне число N <=100 і виводить єдине число – шукану величину.
Приклад
Введення 4
Виведення 10 
Задача Streamer


 

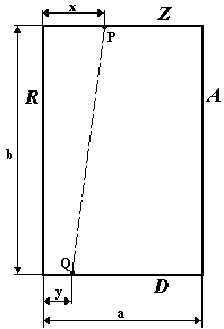
Сторони прямокутного листка паперу позначено  A,R,Z,D. Довжина сторін Z і D - a , довжина сторін A і R - b сантиметрів. На стороні Z, в x сантиметрах від сторони R, розміщено точку P, а на стороні D, в   y  сантиметрах  від  сторони R, розміщено точку Q.
Листок зігнули по лінії  PQ. Знайдіть площу, яку покриває зігнутий листок.
Технічні умови

Програма Streamer  читає з клавіатури числа a, b, x, y.  (a, b, <= 1000) і виводить на екран шукану площу без заокруглень

 

Приклад: 

Введення

5 999 3 3 

Виведення

2.9970000000E+3

.  








 

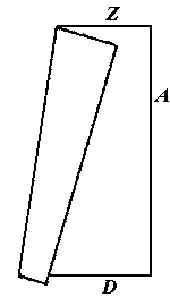
Задача Treasure
 
В пошуках  раніше закопаного скарбу піратам довелось прорити підземний хід в вигляді незамкнутої ламаної, всі відрізки якої лежать на одній глибині. Скарб було знайдено в кінці цієї ламаної. Знайдіть найкоротший шлях, яким пірати можуть винести скарб на її початок, тобто до початку тунелю.
Технічні умови. Програма  Treasure читає з клавіатури кількість відрізків ламаної n,(1<=n<=25)  а далі   n+1 пару цілих чисел, що не перевищують по модулю 1000 – координати вершин ламаної в порядку обходу (перша пара – координата початку ламаної, остання – кінця). Програма виводить на екран єдине дійсне число (без округлення) – шуканий шлях
Приклад
Введення  3  2  2  10 8 10 2 2 8
Виведення 10.000000000

Завдання підготували А. Коротков, Г. Непомнящий, І. Порубльов, Ю. Пасіхов

© LIKT 1998-2024