Завдання фінального туру NetOI-2019
Задача Decentralization. Реформа децентралізації добре вплинула на кількість грошей, які місцева влада може віддати на важливі проекти. Однак не усі міста користуються популярністю серед туристів, а влада прагне якомога збільшити привабливість країни загалом, тому відмітила з усіх N міст рівно K найпопулярніших. Державні експерти порекомендували усім міським головам у разі необхідності “поділитися” їх місцевими бюджетами з іншими містами(*), аби ті могли розвинути туристичний сектор, а також поставили чітку метрику привабливості країни - мінімальний серед бюджетів, виділених на розвиток популярних міст.
Вас же просять допомогти з визначенням максимального показника цієї метрики цього року, з урахуванням поточних запланованих бюджетів.
Примітки
*) за новими антикорупційними правилами, частина бюджету може перейти з одного міста в інше лише у випадку, коли хоча б одне з них туристично популярне (тобто є у тому самому списку з К міст), а крім того між цими двома містами укладено договір співпраці. При цьому ліміту на “переливання” коштів немає (окрім того, що бюджет не має “піти в мінус”). Крім того, дозволяється ділитися лише цілою кількістю гривень.
Технічні умови Програма Decentralization читає з першого рядка стандартного пристрою введення три числа - N та K (1 ≤ K ≤ N ≤ 10’000), а також кількість договорів співпраці M (0 ≤ M ≤ N * (N - 1) / 2). З другого рядка слід прочитати рівно K різних чисел, кожне з яких у межах від 1 до N - відмічені міста. Далі, з третього рядка, програма читає ще N чисел - бюджети міст, кожне число від 0 до 106, i-те число задає бюджет i-го міста. Далі слідують рівно M пар чисел, які задають договори співпраці у форматі Ai Bi, що означає, що між містами Ai та Bi укладено договір.
Програма виводить єдине число - максимальну досяжну метрику, тобто найбільше можливе значення мінімального бюджету серед “популярних” міст після необхідних переливань.
Приклади
|
Введення |
Виведення |
Пояснення |
|
3 2 2 1 3 3 3 3 1 2 2 3
|
4 |
З другого міста можна віддати по 1 гривні у перше та третє місто, після чого їх бюджети будуть рівними - по 4 гривні. При цьому, навіть якщо останню гривню бюджету другого міста віддати якомусь іншому, збільшити метрику не вдасться - адже мінімальний з бюджетів однак буде рівний 4. |
|
3 2 2 2 3 6 0 4 1 2 2 3 |
5 |
Можна перевести з першого міста у друге усі 6 гривень бюджету, після чого з другого у третє перевести 1 гривню. Після цього мінімальне значення бюджету серед популярних міст стане рівним 5. |
Задача Forum. На форумі однієї маленької, але дуже гордої олімпіади є тема, присвячена обговоренню правил. Вона містить N сторінок, пронумерованих от 1 до N. Заходячи в тему, користувач потрапляє на сторінку з номером 1. Інтерфейс користувача (UI) на форумі організовано таким чином, що з сторінки з номером i можливо за один клік перейти на сторінки з номерами i-1 (якщо i>1), i+1 (якщо i<N), 1, N, floor((1+i)/2), ceil((i+N)/2).* Аналіз активності сайту показав, що в темі користувач виконує не більше K кліків. Адміністрацію олімпіади цікавить, скільки сторінок теми за таких умов взагалі хтось зможе прочитати.
Технічні умови. Програма Forum читає з пристрою стандартного введення 2 цілих числа, N (1≤N≤2*108) і K (0≤K≤106). Програма виводить єдине ціле число - кількість сторінок, які можна прочитати за K або менше кліків.
Приклад
Введення
10 1
Виведення
4
*)Примітка: floor((1+i)/2) – найбільше ціле число, що не перевищує (1+i)/2
ceil((i+N)/2) – найменше ціле число, що не менше за (i+N)/2
Задача HardWay. Не «ведіться» на назву задачі. Навпаки, на цьому тест-драйві водієві нового позашляховика доведеться їхати зовсім не по твердому покриттю, а навпаки, по рівнині, яка покрита піском. Вся рівнина розбита паралельними осі Х прямими на своєрідні полоси-зони. В межах кожної зони однорідний, але різний для кожної зони шар піску. Відповідно для кожної полоси є реально досяжна двигуну максимально дозволена швидкість руху. Зрозуміло, що N - 1 горизонтальна пряма задає розмежування N таких зон. Крім того, задані координати початкового і кінцевого пунктів маршруту.
Вам необхідно знайти мінімальний можливий час тест-драйву.
Технічні умови Програма HardWay читає з пристрою стандартного введення у першому рядку число N (2 ≤ N ≤ 30) - кількість зон на мапі. З наступного рядка програма читає N - 1 число yi, що задають прямі y = yi - межі зон (i-та пряма задає межу між i та i+1 зонами). З третього рядка програма читає чотири числа xA yA xB yB - координати початкової і кінцевої точок маршруту. Усі числа натуральні і задовольняють нерівність: 0 < yA < y1 < y2 < … < yN-1 < yB ≤ 100’000, xA ≤ 100’000, xB ≤ 100’000. З четвертого рядка програма читає N чисел Vi – максимально можливі швидкості у кожній з N зон. При цьому 1 ≤ Vi ≤ 10000. Швидкості подано у порядку подолання зон.
Програма виводить рівно одне дійсне число - мінімальний час, необхідний на шлях між пунктами A та B за умови руху по кожній зоні з максимально можливій для неї швидкості. Відповідь буде зараховано, якщо абсолютна чи відносна похибки складуть не більш як 10-6.
Приклади
|
Введення |
Виведення |
Коментар |
|
|
2 2 1 1 1 22 1 20 |
2.0000000 |
Оптимальним буде рух по прямій - тоді у першій зоні буде подолано 1 одиницю шляху (зі швидкістю 1), у другій 20 одиниць (зі швидкістю 20), усього 2 одиниці часу. |
|
|
3 5 11 1 1 15 15 3 4 3 |
5.8333333 |
Відображено (див.малюнок) оптимальний маршрут. Витрачений час при цьому складе 5/3 + 10/4 + 5/3 = 35/6, тобто 5,8(3) |
|
Задача Spiral. Числа натурального ряду вписані в клітинки площини по спіралі, так що 1 вписано в клітинку (0,0), 2 - в (1,0), 3 - (1,1) і т. д. Знайти суму, по модулю 1000000007, чисел, що лежать (включно) в прямокутнику, сторони якого паралельні осям, з кутами в (x0, y0) і (x1, y1).
Технічні умови. Програма Spiral читає зі стандартного пристрою введення 4 цілих числа: x0, y0, x1, y1 (-109≤x0≤x1≤109, -109≤y0≤y1≤109). Програма виводить на станда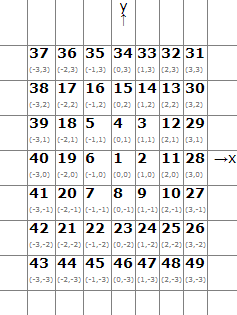 ртний пристрій виведення єдине число - шукану суму по модулю.
ртний пристрій виведення єдине число - шукану суму по модулю.
Приклад.
Введення -1 1 2 3
Виведення 216
Коментар до прикладу. Прямокутник -1≤x≤2 , 1≤y≤3 містить 12 клітинок. Їх сума 5+4+3+12+16+15+14+13+35+34+33+32=216.
Задача Status. В одній дуже відомій в колах учасників NetOI комп’ютерній грі герой і монстр мають такі властивості: HP (здоров'я), Atk (атака), Def (захист), Spd (швидкість). Бій між ними відбувається наступним чином: у кого вище Spd - ходить першим; при рівних Spd - першим ходить монстр – в нього був час підготуватися, поки герой до нього дістався. За один хід гравець HP супротивника "наносить йому втрати" на величину різниці своєї Atk і його Def (якщо ця величина додатна, інакше HP суперника не змінюється). Бій закінчується, коли здоров’я одного з учасників падає до 0 або нижче. Визначте, на яку найменшу кількість пунктів (сумарно) потрібно герою збільшити параметри (кількість пунктів - це сума 4-х (цілих, невід’ємних) доданків до HP, Atk, Def, Spd відповідно) перед боєм, щоб перемогти (коли в кінці поєдинку HP героя буде додатним, а монстра 0 або нижче).
Технічні умови. Програма Status читає з пристрою стандартного введення 8 натуральних чисел не більших 999999999: спочатку 4 параметри героя (в порядку HP, Atk, Def, Spd), далі 4 параметри монстра (у тому ж порядку). Програма виводить на стандартне пристрій виводу єдине ціле число - мінімально необхідне сумарне число пунктів, які потрібно до початку бою десь роздобути герою для перемоги.
Приклад
Введення: 10 7 4 10 29 10 2 5
Виведення: 5
Коментар до прикладу. У початковій ситуації герой наносить монстру 7-2 = 5 пунктів втрат за 1- хід, а монстр герою - 10-4 = 6 (герой ходить першим). Таким чином, через 2 ходи кожного суперника, здоров’я героя знижується до -2, а у монстра ще залишається 19. Але якщо підвищувати захист героя на 5 пунктів, то монстр буде наносити герою 10- (4 + 5) = 1 втрату за хід, і тоді після 6-ти ходів героя (і 5 монстра) здоров’я монстра знижується до -1, а у героя ще залишився 5.
Завдання підготували М.Авраменко В.Бездушний, Г.Непомнящий, Ю.Пасіхов, Д.Поліщук, М.Стречень