ЗАДАНИЯ ФИНАЛЬНОГО ТУРА NetOI-2019
Задача Decentralization. Реформа децентрализации хорошо повлияла на количество денег, которые местная власть может отдать на важные проекты. Однако не все города пользуются популярностью среди туристов, а власть стремится максимально увеличить привлекательность страны в целом, потому отметила из всех N городов ровно K самых популярных. Государственные эксперты порекомендовали всем мэрам городов в случае необходимости "поделиться" их местными бюджетами с другими городами (*), чтобы те могли развить туристический сектор, а также поставили четкую метрику привлекательности страны - минимальный среди бюджетов, выделенных на развитие популярных городов.
Вас же просят помочь с определением максимального показателя этой метрики в этом году, с учетом текущих запланированных бюджетов.
Примечания
*)по новым антикоррупционным правилам, часть бюджета может перейти из одного города в другой лишь в случае, когда хотя бы один из них туристически популярный (то есть имеется в том же списке из К городов), а кроме того между этими двумя городами заключен договор сотрудничества. При этом лимита на "переливание" средств нет (кроме того, что бюджет не должен "пойти в минус"). Кроме того, разрешается делиться только целым количеством гривен.
Технические условия. Программа Decentralization читает с первой строки стандартного устройства ввода три числа - N и K (1 ≤ K ≤ N ≤ 10'000), а также количество договоров сотрудничества M (0 ≤ M ≤ N * (N - 1) / 2). Со второй строки следует прочитать ровно K различных чисел, каждое из которых в пределах от 1 до N - отмеченные города. Дальше, с третьей строки, программа читает еще N чисел - бюджеты городов, каждое число от 0 до 106, i- тое число задает бюджет i- го города. Дальше следуют ровно M пар чисел, которые задают договоры сотрудничества в формате Ai Bi, что означает, что между городами Ai и Bi заключен договор.
Программа выводит единственное число - максимальную досягаемую метрику, то есть наибольшее возможное значение минимального бюджета среди "популярных" городов после необходимых переливаний.
Примеры
|
Ввод |
Вывод |
Пояснения |
|
3 2 2 1 3 3 3 3 1 2 2 3
|
4 |
Из второго города можно отдать по 1 гривне в первый и третий город, после чего их бюджеты будут равными - по 4 гривни. При этом, даже если последнюю гривну бюджета второго города отдать кому-то другому, увеличить метрику не удастся - ведь минимальный из бюджетов все равно будет равен 4. |
|
3 2 2 2 3 6 0 4 1 2 2 3 |
5 |
Можно перевести из первого города во второй все 6 гривен бюджета, после чего из второго в третий перевести 1 гривну. После этого минимальное значение бюджета среди популярных городов станет равным 5. |
Задача Forum. На форуме одной маленькой, но очень гордой олимпиады есть тема, посвященная обсуждению правил. Она содержит N страниц, пронумерованных от 1 до N. Заходя в тему, пользователь попадает на страницу с номером 1. Интерфейс пользователя (UI) на форуме организован таким образом, что из страницы с номером i возможно за один клик перейти на страницы с номерами i - 1 (если i>1), i+1 (если i<N), 1, N, floor ((1+i)/2), ceil ((i+N)/2).* Анализ активности сайта показал, что в теме пользователь выполняет не больше K кликов. Администрацию олимпиады интересует, сколько страниц темы при таких условиях вообще кто-то сможет прочитать.
Технические условия. Программа Forum читает с устройства стандартного ввода 2 целіх числа, N (1≤N≤2*108) и K (0≤K≤106). Программа выводит единственное целое число - количество страниц, которые можно прочитать за K либо меньше кликов.
Пример
Ввод
10 1
Вывод
4
*)Примечание: floor((1+i)/2) – наибольшее целое число, не превосходящее (1+i)/2
ceil((i+N)/2) – наименьшее целое число, не меньшее (i+N)/2
Задача HardWay. Не "ведитесь" на название задачи. Напротив, на этом тест-драйве водителю нового внедорожника придется ехать вовсе не по твердому покрытию, а наоборот, по равнине, покрытой песком. Вся равнина разбита параллельными оси Х прямыми на своеобразные полосы-зоны. В пределах каждой зоны однородный, но разный для каждой зоны слой песка. Соответственно для каждой полосы реально достижима двигателю максимально разрешенная скорость движения. Очевидно, что N - 1 горизонтальная прямая задает разграничение N таких зон. Кроме того, заданы координаты начального и конечного пунктов маршрута.
Вам необходимо найти минимальное возможное время тест-драйва.
Технические условия. Программа HardWay читает с устройства стандартного ввода в первой строке число N (2 ≤ N ≤ 30) - количество зон на карте. Со следующей строки программа читает N - 1 чисел yi, задающих y = yi - границы зон (i-тая прямая задает границу между i и i+1 зонами). С третьей строки программа читает четыре числа xA yA xB yB - координаты начальной и конечной точек маршрута. Все числа натуральные и удовлетворяют неравенству: 0 < yA < y1 < y2 < … < yN-1 < yB ≤ 100’000, xA ≤ 100’000, xB ≤ 100’000. С четвертой строки программа читает N чисел Vi – максимально возможные скорости в каждой из N зон. При этом 1 ≤ Vi ≤ 10000. Скорости заданы в порядке прохождения зон.
Программа выводит ровно одно действительное число - минимальное время, необходимое на путь между пунктами A и B при условии движения по каждой зоне с максимально возможной для нее скоростью. Ответ будет засчитан, если абсолютная или относительная погрешность составят не более чем 10-6.
Пример
|
Ввод |
Вывод |
Комментарий |
|
|
2 2 1 1 1 22 1 20 |
2.0000000 |
Оптимальным будет движение по прямой - тогда в первой зоне будет пройдено 1 единицу пути (со скоростью 1), во второй 20 единиц (со скоростью 20), всего 2 единицы времени. |
|
|
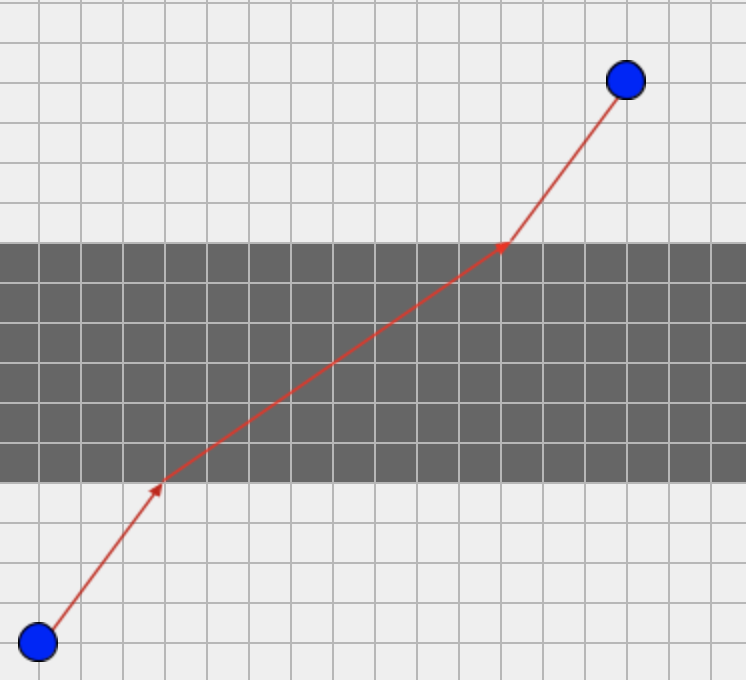
3 5 11 1 1 15 15 3 4 3 |
5.8333333 |
Показано (см.рисунок) оптимальный маршрут. Затраченное время при этом составит 5/3 + 10/4 + 5/3 = 35/6, то есть 5,8(3) |
 |
Задача Spiral. Числа натурального ряда вписаны в клетки плоскости по спирали, так что 1 вписано в клетку (0,0), 2 - в (1,0), 3 - (1,1) и т. д. Найти сумму, по модулю 1000000007, чисел, лежащих (включительно) в прямоугольнике, стороны которого параллельны осям, с углами в (x0, y0) и (x1, y1).
Технические условия. Программа Spiral читает со стандартного устройства ввода 4 целых числа: x0, y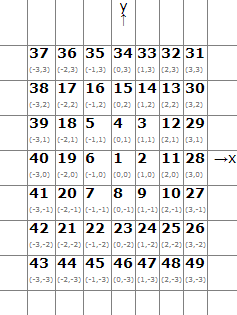
0, x1, y1 (-109≤x0≤x1≤109, -109≤y0≤y1≤109). Программа выводит на стандартное устройство вывода единственное число - искомую сумму по модулю.
Пример.
Ввод -1 1 2 3
Вывод 216
Комментарий к примеру. Прямоугольник -1≤x≤2 , 1≤y≤3 содержит 12 клеток. Их сумма 5+4+3+12+16+15+14+13+35+34+33+32=216.
Задача Status. В одной очень известной в кругах участников NetOI компьютерной игре герой и монстр имеют такие свойства: HP (здоровье), Atk (атака), Def (защита), Spd (скорость). Бой между ними происходит следующим образом: у кого выше Spd - ходит первым; при равных Spd - первым ходит монстр - у него было время подготовиться, пока герой к нему добрался. За один ход игрок HP противника "наносит ему потери" на величину разности своей Atk и его Def (если эта величина положительна, иначе HP соперника не изменяется). Бой заканчивается, когда здоровье одного из участников падает до 0 или ниже. Определите, на какое наименьшее количество пунктов (суммарно) нужно герою увеличить параметры (количество пунктов - это сумма 4-х (целых, неотрицательных) слагаемых к HP, Atk, Def, Spd соответственно) перед боем, чтобы победить (когда в конце поединка HP героя будет положительным, а монстра 0 или ниже).
Технические условия. Программа Status читает с устройства стандартного ввода 8 натуральных чисел не больших 999999999: сначала 4 параметра героя (в порядке HP, Atk, Def, Spd), далее 4 параметра монстра (в том же порядке). Программа выводит на стандартное устройство вывода единственное целое число - минимально необходимое суммарное число пунктов, которые нужно до начала боя где-то раздобыть герою для победы.
Пример
Ввод: 10 7 4 10 29 10 2 5
Вывод: 5
Комментарий к примеру. В начальной ситуации герой наносит монстру 7-2 = 5 пунктов потерь за 1- ход, а монстр герою - 10-4 = 6 (герой ходит первым). Таким образом, через 2 хода каждого соперника, здоровье героя уменьшается до -2, а у монстра еще остается 19. Но если повышать защиту героя на 5 пунктов, то монстр буде наносить герою 10- (4 + 5) = 1 потерю за ход, і тогда после 6-ти ходов героя (і 5 монстра) здоровье монстра снижается до -1, а у героя еще осталось 5.
Завдання підготували М.Авраменко, В.Бездушний, Г.Непомнящий, Ю.Пасіхов, Д.Поліщук, М.Стречень