Маятник (Pendulum)
На уроці фізичного практикуму Василь досліджував роботу математичного маятника. Маятник складається з матеріальної точки, підвішеної на невагомій нерозтяжній нитці. Вася записав на листку координати матеріальної точки маятника у певному хронологічному порядку. Для цього він обрав деяку систему координат, де сила тяжіння направлена у від'ємному напрямку осі OY.
Повернувшись додому, Василь почав обраховувати характеристики маятника, який він досліджував, а саме координати точки підвісу, довжину нитки, та мінімальну кількість повних коливань, що зробив маятник. Допоможіть йому перевірити чи не зробив він помилку, і якщо не зробив, знайдіть координати центру маятника, довжину нитки та мінімальну кількість повних коливань Василь пам’ятає, що він не відхиляв маятник більш, ніж на 90о.
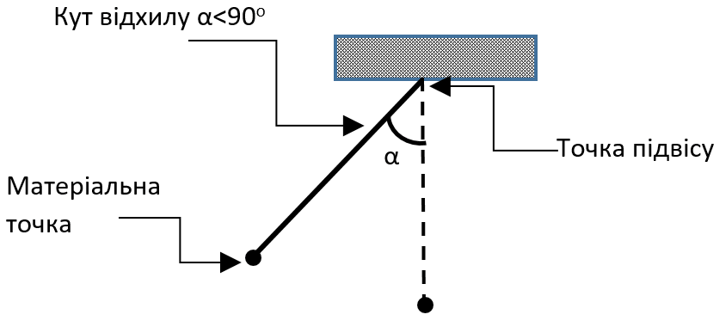
Візьміть до уваги Точка знаходиться на колі, якщо відстань від неї до центру кола відрізняється від радіуса не більше ніж на 10-2.
Технічні умови
Програма Pendulum спочатку зчитує зі стандартного пристрою введення (клавіатури) єдине натуральне число N (3 ≤ N ≤ 107) – кількість точок, що відмітив Василь. У наступних N рядках знаходяться координати самих точок (-106 ≤ x, y ≤ 106), записані через пропуск.
Програма Pendulum виводить на стандартний пристрій виведення (екран) число -1 (мінус один), якщо маятника, що проходить через всі задані точки, не існує. Інакше перший рядок відповіді має містити координати x та y центру маятника, другий рядок – довжину нитки маятника, третій містить мінімальну кількість повних коливань. Дійсні числа вважаємо рівними, якщо модуль різниці між ними не більш ніж 10-2.
Приклад
|
Введення |
Виведення |
|
3 0 3 3 0 6 3 |
3 3 3 1 |
|
4 0 3 3 0 7 4 6 3 |
-1 |
- - - - - - - - - - - - - - - - - - - - - - - - - - - -
Одинички (Onestransform)
У той час як Василь міркував над конструкцією із дзеркал, Миколі було дуже нудно. Він сидів і повільно малював на листочку паперу через кому послідовність одиничок. Врешті-решт йому вдалося написати достатньо довгу послідовність з N одиничок і тут… Еврика! Миколі спало на думку, що з цією послідовністю можна зробити деякі перетворення. Він вирішив замінювати довільну кількість послідовних одиничок числом, що дорівнює кількості замінених одиниць. Очевидно, що таких замін можна зробити дуже багато і, щоб зменшити кількість можливих перетворень, Микола вирішив поставити обмеження на кількість замінюваних одиниць, не більше за k.
Так, наприклад, якщо послідовність містить п’ять одиничок, а k=2, найдовшою заміненою послідовністю може бути послідовність, що містить не більше двох одиниць, тобто 1,1,1,1,1 можна замінити на 2 1 1 1, або на 2 2 1 або на 1 2 2 або на 2 1 2, але не можна на 4 1 або 3 2.
Зверніть увагу, що одиниці замінюються тільки з початкового набору. Одиниці, що є у складі числа, отриманого після перетворення, наприклад 11, 211 або 111, заміні не підлягають.
Технічні умови
Програма Onestransform зчитує з клавіатури (стандартного пристрою введення) два натуральних числа N (1 ≤ N ≤ 107) – кількість одиничок у послідовності та k (1 ≤ k ≤ 107) – число, яке вказує на максимально можливу кількість одиничок, що підлягають заміні (дозволяється замінювати не більше k одиничок).
Програма виводить на екран (стандартний пристрій виведення) єдине число – кількість можливих перетворень по модулю 109 + 7.
Приклад
| Введення | Виведення |
| 4 3 | 7 |
Пояснення до тесту:
Для N=4 послідовність має вигляд: 1,1,1,1. Можливі перетворення такі:
1 1 1 1
1 1 2
1 2 1
2 1 1
3 1
1 3
2 2
- - - - - - - - - - - - - - - - - - - - - - - - - - - -
Чотири числа (fournumbers)
Після проходження всіх станцій квесту, кожна команда отримала по чотири числа – по одному на кожній станції (пам’ятаєте, їх було рівно чотири). Однак випробування на цьому не завершилися! Виявилося, що тепер потрібно у координаційному центрі забрати ще одне число і швидко відповісти на питання: чи можна із чисел, здобутих на станціях, отримати число з координаційного центру? При цьому над чотирма числами можна виконувати арифметичні операції додавання, віднімання або множення у будь-якому порядку та застосовувати дужки для зміни пріоритетів виконання операцій.
Оскільки призовий фонд обмежений, журі потрібно терміново отримати відповіді від усіх команд, щоб правильно розподілити призи.
Формат введення-виведення:
Програма fournumbers спочатку зчитує з клавіатури (стандартного пристрою введення) єдине натуральне число N (1 ≤ N ≤ 50) – кількість команд. Далі слідує N рядків, кожен з яких містить по п’ять натуральних чисел: перше число – це бажаний результат, далі чотири числа (кожне з яких не перевищує 30), над якими потрібно виконувати дії. Гарантується, що результат обчислень не може перевищувати значення 1018.
Програма виводить на екран (стандартний пристрій виведення) N рядків – результати міркувань команд: у випадку, якщо перше число можна отримати, виконуючи дозволені операції над іншими числам рядку, потрібно вивести YES, в протилежному випадку необхідно вивести NO.
Приклад вхідних та вихідних даних
| Введення | Виведення |
|
2 30 1 2 3 4 33 1 2 3 4 |
YES NO |
Пояснення до тесту:
Число 20 можна отримати із даних чисел наступним чином: 30=(1+4)*2*3. Число 33 отримати не можна ніяк.
- - - - - - - - - - - - - - - - - - - - - - - - - - - -
Катя та калюжі (puddles)
Одного разу весною Катя задумалася про те, що вона нестерпно хоче поїхати на море. Вона потягнулася до екрану монітору, щоб побачити рекламу відпочинку і… Розлила воду на матрицю розміром M×N. На превеликий жах матриця прямо на очах перетворилася на сушу та водойми. Правда, скупчення води на матриці нерозділене сушею, важко назвати морем, але на калюжу воно дійсно схоже. За одну годину всі клітинки, в яких є вода та суміжні із сушею, висихають, тобто перетворюються на сушу. Таким чином кількість калюж змінюється. Спочатку Катя дуже засмутилася, але потім їй стало цікаво через скільки годин у неї на матриці буде рівно K калюж.
Оскільки Катя не дуже сильний програміст, то цю задачу вона залишає для вас.
Технічні умови
Програма puddles спочатку зчитує зі стандартного пристрою введення (клавіатури) три цілих числа M, N, K (1⩽ M,N ⩽103,1⩽ K ⩽106). Кожен з наступних M рядків буде містити N символів, кожен з яких може бути або d і це означає, що на цьому елементі знаходиться суша, або w – вода. Гарантується, що в матриці Каті, після того як вона розлила воду, є і суша, і вода.
Програма виводить на стандартний пристрій виведення (екран) єдине значення – час, коли в матриці буде рівно K калюж або «No Solution» (без лапок), якщо відповіді не існує.
Приклад
| Введення 1 | Виведення 1 |
|
5 5 3 wwwww wdddw wwdww wwdww wwwww |
No Solution |
| Введення 2 | Виведення 2 |
|
5 9 2 ddddddddd dwwwdwwwd dwwwwwwwd dwwwdwwwd ddddddddd |
1 |
- - - - - - - - - - - - - - - - - - - - - - - - - - - -
Задача Antigrav
План антивсесвіту можливо представити у вигляді декартової площини, де розміщено N планет-точок, кожна з відомою масою. Для кожної точки (x0, y0) площини можливо обчислити індекс антигравітації за наступною формулою:
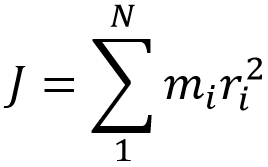
де mi – маса i-ой планети, а ri –відстань від заданої точки до i-ої планети.
Для заданого планом антивсесвіту і індексу антигравітації J треба знайти точку на плані, індекс антигравітації якої дорівнює J.
Технічні умови
Програма Antigrav читає з стандартного пристрою введення (клавіатури) наступні данні:
В першому рядку індекс антигравітації J – натуральне число, що не превищує 1018.
В другому рядку число планет системи N – натуральне число, що не перевищує 106.
Наступні N рядків описують планети в форматі xi yi mi – положення планет на плані і маса планети. При цьому маса кожної планети – натуральное число, що не перевищує 103, а координати по модулю не перевищують 104.
Програма повинна вивести -1 у випадку, якщо шуканої точки не існує. У іншому випадку – координати цієї точки x0 y0. Ваша відповідь не будет зарахована в тому випадку, якщо абсолютна і відносна похибка ,індекса антигравітації в вашій точці буде перевищувати 10-5.
Приклад:
|
Введення |
Виведення |
|
1 2 1 1 10 20 1 20 |
-1 |
|
18 3 1 1 1 3 3 3 4 1 2 |
2.2928932 2.7071068 |


