Маятник (Pendulum)
На уроке физического практикума Василий исследовал работу математического маятника. Маятник состоит из материальной точки, подвешенной на невесомой нерастяжимой нитке. Вася записал на листке координаты материальной точки маятника в определенном хронологическом порядке. Для этого он выбрал некоторую систему координат, сила тяжести направлена в отрицательном направлении оси OY.
Вернувшись домой, Вася начал вычислять характеристики исследуемого маятника, а именно координаты точки подвеса, длину нитки и минимальное количество полных колебаний маятника. Помогите ему проверить, не сделал ли он ошибку, и если не сделал, найдите координаты центра маятника, длину нитки и минимальное количество полных колебаний маятника. Василий помнит, что он не отклонял маятник больше, чем на 90о.
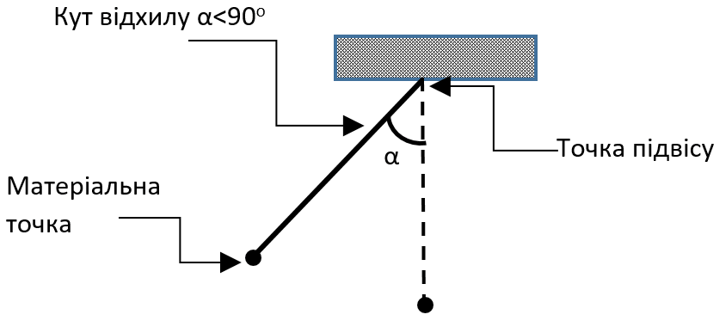
Обратите внимание: Точка находится на круге, если расстояние от нее до центра окружности отличается от радиуса не более чем на 10-2.
Технические условия:
Программа Pendulum сначала считывает со стандартного устройства ввода (клавиатуры ) единственное натуральное число N (3 ≤ N ≤ 107) – количество точек, которые отметил Василий. В следующих N строках находятся координаты самих точек (-106 ≤ x, y ≤ 106), которые записаны через пробел.
Программа Pendulum выводит на стандартное устройство вывода (экран) число -1 (минус один), если маятника, который проходит через все заданные точки, не существует. Иначе первая строка ответа должна содержать координаты x и y центра маятника, вторая – длину нитки маятника, а третья – минимальное количество полных колебаний. Действительные числа считаем равными, если модуль разницы между ними не более 10-2.
Пример
|
Ввод |
Вывод |
|
3 0 3 3 0 6 3 |
3 3 3 1 |
|
4 0 3 3 0 7 4 6 3 |
-1 |
- - - - - - - - - - - - - - - - - - - - - - - - - - - -
Единицы (Onestransform)
В то время, когда Вася работал над конструкцией из зеркал, Коле было очень тоскливо. Он сидел и неторопливо рисовал на листочке через запятую последовательность единиц. В конце концов ему удалось написать достаточно длинную последовательность из N единичек и тут… Эврика! Николаю пришло в голову, что с этой последовательностью можно сделать некоторые преобразования. Он решил заменять произвольное количество последовательных единиц числом, которое равняется количеству замененных единиц. Очевидно, что таких замен можно сделать очень много и, чтобы уменьшить количество возможных преобразований, Коля решил поставить ограничение на количество заменяемых единиц, не превышающее число k.
Так например, когда последовательность содержит пять единиц, а k=2, самой длинной замененной последовательностью может быть последовательность, которая содержит не более двух единиц, т.е. 1,1,1,1,1 можно заменить на 2 1 1 1 либо 2 2 1, либо 1 2 2 либо 2 1 2, но нельзя на 4 1 или 3 2.
Обратите внимание, что единицы можно заменить только из начального набора. Единицы, которые есть в составе числа, полученного после преобразования, например, 11, 211 или 111, замене не подлежат.
Технические условия
Программа Onestransform читает со стандартного устройства ввода (клавиатуры) два натуральных числа N (1 ≤ N ≤ 107) – количество единиц в последовательности и k (1 ≤ k ≤ 107) – число, которое указывает на максимально возможное количество единиц, которые подлежат замене (позволяется заменять не более k единиц).
Программа выводит на стандартное устройство вывода (экран) единственное число – количество возможных преобразований по модулю 109 + 7.
Пример
| Ввод | Вывод |
| 4 3 | 7 |
Пояснения к тесту:
Для N=4 последовательность имеет вид: 1,1,1,1. Возможные преобразования следующие:
1 1 1 1
1 1 2
1 2 1
2 1 1
3 1
1 3
2 2
- - - - - - - - - - - - - - - - - - - - - - - - - - - -
Четыре числа (fournumbers)
После прохождения всех станций квеста, каждая команда получила по четыре числа – по одному на каждой станции (помните, их было ровно четыре). Однако испытания на этом не закончились! Оказалось, что теперь необходимо в координационном центре забрать еще одно число и максимально быстро ответить на вопрос: можно ли из чисел, добытых на станциях, получить число из координационного центра? При этом над четырьмя числами можно выполнять арифметические операции сложения, вычитания или умножения в любом порядке и применять круглые скобки для изменения приоритетов выполнения операций.
Поскольку призовой фонд ограничен, жюри необходимо срочно получить ответы от всех команд, чтобы правильно распределить призы.
Технические условия:
Программа fournumbers сначала читает со (стандартного устройства ввода (клавиатуры) единственное натуральное число N (1 ≤ N ≤ 50) – количество команд. Далее следует N строк, каждая из которых содержит по пять натуральных чисел: первое число – это желаемый результат, далее четыре числа (каждое из которых не превышает 30), над которыми необходимо выполнять действия. Гарантируется, что результат вычислений не может превышать значение 1018.
Программа выводит на стандартное устройство вывода (экран) N строк – результаты выводов команд: в случае, если первое число можно получить, выполняя разрешенные операции над остальными числам строки, необходимо вывести YES, в противном случае – вывести NO.
Пример входных и выходных данных
| Ввод | Вывод |
|
2 30 1 2 3 4 33 1 2 3 4 |
YES NO |
Пояснения к тесту:
Число 20 из заданных чисел можно получить таким образом: 30=(1+4)*2*3. Число 33 получить никак невозможно.
- - - - - - - - - - - - - - - - - - - - - - - - - - - -
Катя и лужи (puddles)
Однажды весной Катя задумалась о том, что она нестерпимо хочет поехать на море. Она потянулась к экрану монитора, чтобы увидеть рекламу отдыха и… Разлила воду на матрицу размером M×N. К сожалению, матрица прямо на глазах превратилась в сушу и водоемы. Правда, скопление воды на матрице не разделенное сушей, трудно назвать морем, но на лужу оно действительно похоже. За один час все клеточки, в которых есть вода и смежные с сушей, высыхают, т.е. превращаются в сушу. Таким образом количество луж изменяется. Сначала Катя очень расстроилась, но потом ей стало интересно через сколько часов у нее на матрице будет ровно K луж.
Поскольку Катя не очень сильный программист, то эту задачу она оставляет для вас.
Формат ввода-вывода:
Программа puddles сначала читает с клавиатуры (стандартного устройства ввода) три целых числа M, N, K (1⩽ M,N ⩽103,1⩽ K ⩽106). Каждая из следующих M строк будет содержать N символов, каждый из которых может быть или d и это означает, что на этом элементе находится суша, или w – вода. Гарантируется, что в матрице Кати, после того как она разлила воду, есть и суша, и вода.
Программа выводит на экран (стандартное устройство вывода) единственное значение – время, когда в матрице будет ровно K луж или «No Solution» (без кавычек), если ответа не существует.
Пример входных и выходных данных
| Ввод 1 | Вывод 1 |
|
5 5 3 wwwww wdddw wwdww wwdww wwwww |
No Solution |
| Ввод 2 | Вывод 2 |
|
5 9 2 ddddddddd dwwwdwwwd dwwwwwwwd dwwwdwwwd ddddddddd |
1 |
- - - - - - - - - - - - - - - - - - - - - - - - - - - -
Задача Antigrav
План антивселенной можно представить в виде декартовой плоскости, где расположены N планет-точек, каждая с известной массой. Для каждой точки (x0, y0) плоскости можно вычислить индекс антигравитации по следующей формуле:
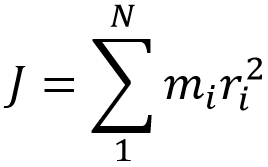
где mi – масса i-ой планеты, а ri – расстояние от заданной точки до i-ой планеты.
Для заданной планом антивселенной и индекса антигравитации J найти точку на плане, индекс антигравитации которой равен J.
Технические условия
Программа Antigrav читает со стандартного устройства ввода (клавиатуры) следующие данные:
В первой строке индекс антигравитации J – натуральное число, не превышающее 1018.
Во второй строке число планет системы N – натуральное число, не превышающее 106.
Следующие N строк описывают планеты в формате xi yi mi – положение планеты на плане и масса планеты. При этом масса каждой планеты – натуральное число, не превосходящее 103, а координаты по модулю не превышают 104.
Программа должна вывести -1 в случае, если искомой точки не существует. В противном случае – координаты этой точки x0 y0. Ваш ответ не будет засчитан в том случае, если абсолютная и относительная погрешность индекса антигравитации в вашей точке будет превышать 10-5.
Примеры:
|
Ввод |
Вывод |
|
1 2 1 1 10 20 1 20 |
-1 |
|
18 3 1 1 1 3 3 3 4 1 2 |
2.2928932 2.7071068 |


