Задача Lens. Семикласник Василько, виконуючи лабораторну роботу з визначення фокусної відстані тонкої збиральної лінзи, встановив, що фокусна відстань його лінзи дорівнює рівно F см. При цьому він помітив, що відстані d см від лінзи до предмета та f см від лінзи до екрана, на якому утворилось чітке зображення предмета, також цілі числа. Василько зацікавився, скількома способами він зможе розмістити предмет і екран на головній оптичній осі лінзи так, щоб на екрані було чітке зображення предмета, а відстані d і f (знову ж таки в сантиметрах) були цілими числами. Досить швидко Василько знайшов відповідь на питання, що його цікавило. Нехай те саме зробить і ваша програма.
Технічні умови Програма Lens читає з пристрою стандартного введення (клавіатури) єдине ціле число F (1 ≤ F ≤ 1016 );
Програма виводить на пристрій стандартного виведення (екран) єдине число – шукану величину.
Приклади
Введення 3
Виведення 3
Пояснення до прикладів: для лінзи з фокусною відстанню 3 см існує три способи розміщення:
|
d, см |
f, см |
|
4 |
12 |
|
6 |
6 |
|
12 |
4 |
Примітка. Якщо F – фокусна відстань лінзи, d - відстань від лінзи до предмета, f - відстань від лінзи до зображення предмета, то формула тонкої лінзи запишеться у вигляді:
.
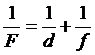(хоча це повинен знати кожен семикласник)
Задача Sweets. Сергій дуже любить цукерки, а тому ніколи не допустить їх псування. Він купив 
різних за смаком цукерок, які планує з’їсти за 
день. Сергій розклав всі цукерки в ряд та послідовно пронумерував їх від 1 до N. Першого дня хлопець з’їсть менш смачну з цукерок з номерами 1 та 2, далі - менш смачну із пари з номерами 3 та 4 і т.д., менш смачні (N-1)-ої та N-ої пар , більш смачна цукерка з кожної пари залишиться лежати на столі. Другого дня Сергій пронумерує цукерки, що залишилися, від 1 до 
й аналогічним чином обиратиме та їстиме цукерки. В останній ()-ий день залишиться лише одна цукерка, яку Сергій просто з’їсть.Пронумеруємо цукерки за їхніми смаковими якостями від 1 до N (1 – найбільш смачна, N – найменш смачна). Сергій хоче розкласти цукерки в ряд так, щоби в кожен з днів, до того як він почне їх їсти, на столі лежали найсмачніші цукерки (тобто, якщо в якийсь день на столі лежить n цукерок, то це мають бути n найсмачніших цукерок).
Технічні умови. Програма Sweetsчитає з клавіатури (стандартного введення) число N – кількість цукерок, гарантується що N – степінь двійки та 
. Програма виводить на екран N чисел, i-те з яких буде номером цукерки, що має лежати на i-ому місці. Якщо існує кілька оптимальних відповідей, виведіть будь-яку з них.
Приклад
Задача Divide. До дідуся приїхали онуки: Катерина і Дмитро. Дідусь підготував їм подарунок - коробку з відеофільмами, але сказав, що в коробці парна кількість дисків з фільмами, які він поділити не зміг, але хотів би, аби половина дісталась Катрусі й половина Дмитру. Діти придумали досить цікавий спосіб поділу: спочатку вони читали опис кожного фільму, а потім ставили якусь оцінку цьому фільму (кожен свою, оцінки того ж фільму можуть відрізнятись). Потім вони склали всі фільми в коробку. Дмитро витягував кожного разу два диски, і, як справжній джентльмен, давав Катерині вибрати один собі, а інший забирав сам. Зрозуміло, що Катерина обирала той фільм, в якого її оцінка більша. Але Дмитро бажав, щоб сума його оцінок отриманих ним фільмів була якомога більшою. Оскільки він пам'ятав всі свої оцінки й всі оцінки Катерини, Дмитро, підглядаючи у коробку, обирав по два диски кожного разу таким чином,аби в кінці сума його оцінок отриманих ним фільмів була найбільшою.
Технічні умови. Програма Divide читає з клавіатури (стандартного введення) натуральне число N (2≤N≤5000, N - парне). Далі програма читає з наступного рядка оцінки Катерини - N натуральних чисел (до того ж, всі оцінки Катерини різні). З третього рядка програма читає ще N чисел - оцінки Дмитра. Гарантується, що оцінки лежать в межах від 1 до 400000 включно. Програма виводить N/2 рядків по два числа через пропуск, в кожному - пари фільмів, в тому порядку, в якому їх треба витягувати Дмитру. Фільми нумеруються з одиниці. Числа в кожному рядку можна виводити в довільному порядку. Якщо існує декілька рішень, виведіть будь-яке.
Приклади
|
Введення |
Виведення |
|
6 6 10 11 18 5 14 1 7 6 12 15 16 |
5 1 2 3 6 4 |
|
6 6 44 2 43 7 48 6 44 2 43 7 48 |
3 1 5 4 2 6 |
Задача MaxDivs3. Напишіть програму, яка шукатиме максимальну кількість дільників серед усіх чисел вигляду N3–N для всіх N з проміжку A≤N≤B.
Технічні умови. Програма MaxDivs3 читає зклавіатури два числа A, B (2≤A≤B≤2097151=221–1). Програма виводить на екран єдине число - знайдену максимальну кількість дільників.
Приклад
Введення
7 10
Виведення
30
Пояснення. 73–7=336 має 20 дільників, 83–8=504 має 24 дільники, 93–9=720 має 30 дільників, 103–10=990 має 24 дільники, а max(20,24,30,24)=30.
1) За один хід можна зменшити будь-який розряд запису числа у системі числення з основою k на будь-яке ціле значення від 1 до r, але так, щоб значення розряду не стало менше нуля.
2) Перемагає дівчинка, після ходу якої число перетвориться у нуль.
Визначте, хто з дівчат переможе при оптимальній грі обох. Гравці ходять по черзі, перший хід робить Даринка.
Технічні умови. Програма читає з клавіатури натуральне число t (1≤t≤500) - кількість тестових наборів. Наступні t рядків містять по 3 числа, записані через пропуск - початкове число n (1≤n≤1018), основу системи числення k (2≤k≤1018) та r (1≤r≤1018). Програма виводить екран t рядків, кожен з яких повинен містити число 1, якщо переможе Даринка, або 2, якщо переможе Тетянка.
Приклад
Введення
3
123 10 4
7 2 2
48 10 3
Виведення
2
1
2