Задача DYVAKNET
Є N комп’ютерів, занумерованих натуральними числами від 1 до N. Розміщені ці комп’ютери в офісі пана Дивака, де не місце стандартним топологіям комп’ютерних мереж. Тому кабелі не ведуть від комп’ютерів до концентраторів (свічів), а з’єднують пари комп’ютерів. Для цього у комп’ютери вставлено по кілька мережевих карт (від 1 до 8). Кожен кабель симетричний, тобто, зв’язуючи k-ий комп’ютер з j-им, зв’язує також і j-ий з k-им. Відомо, що від кожного комп’ютера до кожного існує хоча б один маршрут (який може проходити через проміжні комп’ютери). Природно виникає бажання взнати для кожної пари комп’ютерів маршрут, що проходить через мінімальну кількість проміжних комп’ютерів. Але пану Диваку мало знати один з мінімальних маршрутів – він бажає знати всі.
Напишіть програму, яка знайде всі маршрути між заданими комп’ютерами, які містять однакову мінімальну кількість проміжних комп’ютерів. Маршрути вважаються різними, якщо відрізняються (не дорівнюють одна одній) послідовності проміжних комп’ютерів. Згідно стандартного означення, що послідовності (a1, a2, …, am) та (b1, b2, …, bm) дорівнюють одна одній лише тоді, коли мають однакову довжину та (a1=b1) and (a2=b2) and … and (am=bm).
Технічні умови.
Програма DYVAKNET читає зі стандартного входу (клавіатури) спочатку кількість комп’ютерів N (3≤N≤128), потім кількість кабелів M (N≤M≤4N), далі M пар чисел від 1 до N кожне — номери комп’ютерів, які з’єднує відповідний кабель. Далі йде остання пара різних чисел від 1 до N кожне – номери комп’ютера-старта та комп’ютера-фініша. Старт і фініш не з’єднані безпосередньо. Всі числа записані в одному рядку й розділені одинарними пробілами.
Програма виводить на стандартний вихід (екран) маршрути — послідовності номерів проміжних комп’ютерів. Кожен маршрут слід виводити в окремому рядку, розділяючи номери комп’ютерів всередині маршруту пропусками. Після останнього маршруту треба вивести порожній рядок. Вказувати кількість маршрутів (рядків) не потрібно. Виводити маршрути можна у довільному порядку, але важливо, щоб усі правильні були вказані рівно по одному разу й не був вказаний жоден неправильний. У рядках дозволяються зайві пропуски, але зайві порожні рядки заборонені. Гарантовано, що розміри правильних відповідей не перевищуватимуть 64 Kb.
Приклад
Введення
5 5 5 4 4 3 3 1 1 2 2 4 1 5
Виведення
2 4
3 4
Задача PlumsGarden
Сливовий сад відомого з задачі Plums фермера Василя П. – прямокутна ділянка довжиною m та шириною n метрів (1≤ m, n ≤1000). Ділянку розбито на квадрати 1х1 м, в центрі кожного з яких росте одна слива.
Сусід Петро допомагав Василеві не тільки у перевезенні вирощеного врожаю, а й стеріг сад від бажаючих поласувати чужими сливами. Сусіди домовились, що в якості плати за виконану роботу Петро вибере довільним чином прямокутну ділянку в межах садка розміром a х b одиничних квадратів. Границі ділянки паралельні границям саду.
Якщо весь урожай слив з цієї ділянки (без остатку) він помістить в кузов своєї вантажівки, то зможе забрати його собі. Петру відома вантажопідйомність p (1≤ p≤109 ) його автомобіля (в кг), а також маса слив на кожному дереві (в кг).
Петро хоче знати, яку найбільшу масу слив W він зможе отримати та кількість k способів вибору ділянки a x b з такою масою слив. Допоможіть Петру.
Технічні умови .
Програма PlumsGarden повинна прочитати з клавіатури в першому рядку натуральні числа m , n , a, b та p (саме в такому порядку!), наступні m рядків містять по n натуральних чисел, кожне з яких не перевищує 32767 – маси слив на кожному з дерев. Числа в рядках розділено пропусками.
Програма PlumGarden повинна вивести на екран цілі числа W та k , записані в один рядок через пропуск.
Приклад
Введення
3 3 2 1 10
1 8 5
5 10 1
4 7 6
Виведення
9 2
 Задача Spider
Задача Spider
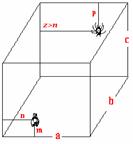
У кімнаті довжиною а, шириною b і висотою с метрів на стіні довжиною а сидить муха на відстані m метрів від підлоги і n метрів від бічної стіни. На протилежній стіні, на відстані р метрів від стелі, сидить павук.
Відстань між комахами така, що муха по прямій лінії зі швидкістю n м/с пролетіла б її на t секунд швидше (t = 0.0abc), ніж, якби павук знаходився від неї на максимально можливому за даних умов віддаленні. Як тільки павук рушає з місця, муха злітає. Яку відстань встигне налітати по кімнаті муха, поки павук буде добиратися до її початкового місця розташування, вибравши шлях, час проходження якого мінімальний? При цьому швидкість павука по стелі в a разів, по стінам в b, а по підлозі в c разів менша швидкості польоту мухи. Гарантовано, що z>n (див. рисунок). Кімната має форму прямокутного паралелепіпеда. Розмірами мухи і павука слід нехтувати. Рух мухи в повітрі і павука по стінах, стелі і підлозі вважати рівномірним.
Технічні умови.
Програма Spider читає зі стандартного входу (клавіатури) шість розділених пропуском натуральних чисел a, b, c, m, n, p (1 < a, b, c < 10); (1 ≤ m, p ≤ c / 2); (1 ≤ n ≤ a / 2). Значення t задається як t = 0.0abc, де a, b, c - цифри відповідних розрядів (тобто, якщо a=7, b=2, c=3, то t=0.0723).
Програма виводить на стандартний вихід (екран) дійсне число (з максимально можливою точністю) - шлях мухи в метрах.
Приклад
Введення
7 7 7 1 2 3
Виведення
88.54982144584919
Задача ATM
Правда, вам набридли абсолютно неприродні олімпіадні задачі? Ну навіщо казати: «Якби банкомат заправили банкнотами по 10, 50 і 60 рублів, то суму 120 варто було б видавати не як 100+10+10, а як 60+60…» Ніхто ж не стане вводити в обіг банкноти номіналом 60… Тому зараз пропонуємо розв’язати абсолютно практичну задачу.
В обігу перебувають банкноти номіналами 1, 2, 5, 10, 20, 50, 100, 200 та 500 гривень. Причому, банкноти номіналами 1 грн та 2 грн в банкомати ніколи не кладуть. Так що в банкоматі є N5 штук банкнот по 5 грн, N10 штук банкнот по 10 грн, N20 штук банкнот по 20 грн, N50 штук банкнот по 50 грн, N100 штук банкнот по 100 грн, N200 штук банкнот по 200 грн та N500 штук банкнот по 500 грн. Для банкомата діють адміністративне обмеження «видавати не більш як 2000 грн за один раз» та технічне обмеження «видавати не більш як 40 банкнот за один раз». В останньому обмеженні мова йде про сумарну кількість банкнот (можливо, різних номіналів).
Напишіть програму, яка визначатиме, як видати потрібну суму мінімально можливою кількістю банкнот (з урахуванням указаних обмежень).
Технічні умови.
Програма ATM читає з пристрою стандартного введення (клавіатури) спочатку кількості банкнот N5, N10, N20, N50, N100, N200 та N500, потім суму S, яку треба видати. Усі числа вхідних даних є цілими, перебувають в межах від 0 включно до 5000 включно.
Програма повинна вивести на пристрій стандартного виведення(екран) сім чисел — скільки треба видати банкнот по 5 грн, по 10 грн, по 20 грн, по 50 грн, по 100 грн, по 200 грн та по 500 грн. Ці сім чисел треба вивести в один рядок, розділяючи пропусками. Сума цих чисел (загальна кількість банкнот до видачі) повинна бути мінімально можливою. Якщо видати суму, дотримуючись обмежень, неможливо, програма повинна замість відповіді вивести -1.
Приклади
Введення
0 100 1 100 0 0 0 190
Виведення
0 2 1 3 0 0 0
Введення
5000 2000 5000 2000 5000 2000 500 17
Виведення
-1
Задача Pifagor
Для того, щоб краще вивчити геометрію, Петро вирішив почати з найпростіших геометричних фігур – трикутників. Особливо його зацікавили прямокутні трикутники, і він почав їх шукати всюди.
Нагадаємо, що трикутник є прямокутним, якщо один із його кутів рівний 90 градусів. Якось Петро побачив на класній дошці n точок і його зацікавило, скільки знайдеться трійок із цих точок, на яких можна побудувати прямокутні трикутники. Допоможіть йому задовольнити цікавість.
Технічні умови
Програма читає зі стандартного входу (клавіатури) ціле число n (3 ≤ n ≤ 1000) та n пар цілих чисел - xi та yi — координати i-ой точки. Координати точок не перевищують 30000 за абсолютним значенням. Всі точки різні.
Програма виводить на стандартний вихід (екран) кількість трійок точок, на яких можна побудувати прямокутні трикутники.
Приклад
Введення
4 0 0 0 1 2 0 0 -4
Виведення
3
Завдання підготували B.Боднар, В.Ластовецький, Г.Непомнящий, Ю.Пасіхов, І. Порубльов


