Задача DYVAKNET
N компьютеров пронумерованы натуральными числами от 1 до N. Они расположены в офисе господина Дывака, где нет места стандартным топологиям компьютерных сетей. Поэтому кабеля не соединяют компьютеры с концентраторами (свичами), а связывают компьютеры попарно. При этом в каждом компьютере установлено несколько сетевых карт (от 1 до 8). Каждый кабель является симметричным, то есть, соединяя k-ый компьютер с j-ым, он соединяет также и j-ый с k-ым.
Известно, что каждая пара компьютеров объединена между собой хотя бы одним маршрутом (который может проходить через промежуточные компьютеры). Естественным является желание узнать для каждой пары компьютеров маршрут, проходящий через минимальное количество промежуточных компьютеров. Но господин Дывак желает узнать не один из минимальных маршрутов, а все.
Напишите программу, которая найдет все маршруты между заданными компьютерами, содержащие одинаковое минимальное количество промежуточных компьютеров. Маршруты считаются разными, если отличаются (не равны друг другу) последовательности промежуточных компьютеров. Согласно стандартному определению, последовательности (a1, a2, …, am) и (b1, b2, …, bm) равны друг другу только тогда, когда имеют одинаковую длину и (a1=b1) and (a2=b2) and … and (am=bm).
Технические условия.
Программа DYVAKNET читает со стандартного входа (клавиатуры) сначала количество компьютеров N (3≤N≤128), потом количество кабелей M (N≤M≤4N), после этого M пар чисел от 1 до N каждое — номера компьютеров, которые соединены соответствующим кабелем. Далее следует последняя пара разных чисел от 1 до N каждое – номера компьютера-старта и компьютера-финиша. Старт и финиш не соединены непосредственно. Все числа записаны в одну строку и разделены одинарными пробелами.
Программа выводит на стандартный выход (экран) маршруты — последовательности номеров промежуточных компьютеров. Каждый маршрут нужно выводить отдельной строкой, разделяя номера компьютеров между собой пробелами. После последнего маршрута нужно вывести пустую строку. Указывать количество маршрутов (строк) не нужно. Выводить маршруты можно в произвольном порядке; важно, чтобы все правильные были указаны ровно один раз и не было ни одного неправильного. В строчках разрешены лишние пробелы, но лишние пустые строки запрещаются. Гарантируется, что размеры правильных ответов не превышают 64 Kb.
Пример
Ввод
5 5 5 4 4 3 3 1 1 2 2 4 1 5
Вывод
2 4
3 4
Задача PlumsGarden
Сливовый сад известного из задачи Plums фермера Василия П. – прямоугольный участок длиной m и шириной n метров (1≤m, n≤1000). Участок разбит на квадраты 1х1 м, в центре каждого из которых растет одна слива.
Сосед Петр помогал Василию не только при перевозке выращенного урожая, но и сторожил сад от желающих полакомиться чужыми сливами. Соседи договорились, что в качестве оплаты за выполненную работу Петр выберет произвольным образом прямоугольный участок в пределах сада размером a х b единичных квадратов. Границы участка параллельны границам сада.
Если весь урожай слив, собранный с этого участка (без остатка) он водворит в кузов своего грузовика, то сможет забрать его себе. Петр знает грузовместимость p (1≤p≤109) его автомобиля (в кг), а также масса слив на каждом дереве (в кг).
Петр хочет узнать, какою наибольшую массу слив W он сможет получить и количество k способов выбора участка a x b с такой массой слив. Помогите Петру.
Технические условия.
Программа PlumsGarden читает со стандартного входа (клавиатуры) в первой строке натуральные числа m, n, a, b и p (именно в таком порядке!), следующие m строк содержат по n натуральных чисел, каждое из которых не превышает 32767 – массы слив на каждом дереве. Числа в строках разделены пробелами.
Программа PlumGarden должна вывести на стандартный выход (экран) целые числа W и k в одну строку через пробел.
Пример
Ввод
3 3 2 1 10
1 8 5
5 10 1
4 7 6
Вывод
9 2
 Задача Spider
Задача Spider
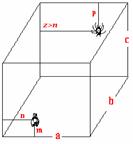
В комнате длиной а, шириной b и высотой с метров на стене длиной а сидит муха на расстоянии m метров от пола и n метров от боковой стены. На противоположной стене, на расстоянии р метров от потолка сидит паук.
Расстояние между насекомыми таково, что муха пролетела б его по прямой линии со скоростью n м/с на t секунд быстрее (t = 0.0abc) чем, если бы паук находился от нее на максимально возможном при данных условиях отдалении. Как только паук начинает движение, муха взлетает. Какой путь успеет пролететь по комнате муха, пока паук попадет в начальное место расположения мухи, выбирая при этом путь с минимальным временем прохождения? Скорость паука по потолку в a раз, по стенам в b, а по полу в c раз меньше скорости полета мухи. Гарантируется, что z>n (см. рисунок). Комната имеет форму прямоугольного параллелепипеда. Размерами мухи и паука следует пренебречь. Движение мухи в воздухе и паука по стенам, потолку и полу считать равномерными.
Технические условия.
Программа Spider читает со стантартного входа (клавиатуры) шесть разделенных пробелом натуральных чисел a, b, c, m, n, p (1 < a, b, c < 10); (1 ≤ m, p ≤ c / 2); (1 ≤ n ≤ a / 2). Значение t задается в виде t = 0.0abc, где a, b, c – цифры соответствующих разрядов (то есть, при a=7, b=2, c=3 t=0.0723).
Программа выводит на стандартный выход (экран) вещественное число (с максимально возможной точностью) – путь мухи в метрах.
Пример
Ввод
7 7 7 1 2 3
Вывод
88.54982144584919
Задача ATM
Вам надоели абсолютно неестественные олимпиадные задачи, не так ли? Ну, зачем говорить: «Если бы банкомат заправили банкнотами номиналом 10, 50 и 60 рублей, то сумму 120 следовало б выдавать не как 100+10+10, а как 60+60…» Никто не станет вводить в оборот банкноты номиналом 60… По этой причине сейчас Вам предлагается решить абсолютно практическую задачу.
В обороте находятся банкноты номиналами 1, 2, 5, 10, 20, 50, 100, 200 и 500 гривен. При этом, банкоматы не заправляют банкнотами номиналами 1 грн и 2 грн. Таким образом, в банкомате есть N5 штук банкнот по 5 грн, N10 штук банкнот по 10 грн, N20 штук банкнот по 20 грн, N50 штук банкнот по 50 грн, N100 штук банкнот по 100 грн, N200 штук банкнот по 200 грн и N500 штук банкнот по 500 грн. На банкомат распространяются административное ограничение «выдавать единоразово не более 2000 грн» и техническое ограничение «выдавать единоразово не более 40 банкнот». Последнее ограничение относится к суммарному количеству банкнот (возможно, разного номинала).
Напишите программу, которая будет определять, как выдать необходимую сумму, использовав минимальное количество банкнот (с учетом указанных ограничений).
Технические условия.
Программа ATM читает со стандартного ввода (клавиатуры) сначала количество банкнот N5, N10, N20, N50, N100, N200 и N500, потом сумму S, которую нужно выдать. Все числа входных данных – целые и находятся в пределах от 0 включительно до 5000 включительно.
Программа должна вывести на стандартный выход (экран) семь чисел — количества банкнот по 5 грн, по 10 грн, по 20 грн, по 50 грн, по 100 грн, по 200 грн и по 500 грн. Эти семь чисел нужно вывести в одну строку через пробелы. Сумма этих чисел (общее количество банкнот к выдаче) должна быть минимально возможной. Если выдать сумму, учитывая ограничения, невозможно, программа должна вместо ответа вывести -1.
Примеры
Ввод
0 100 1 100 0 0 0 190
Вывод
0 2 1 3 0 0 0
Ввод
5000 2000 5000 2000 5000 2000 500 17
Вывод
-1
Задача Pifagor
Чтоб лучше выучить геометрию, Петр решил начать с самых простых геометрических фигур – треугольников. Особенно его заинтересовали прямоугольные треугольники, он даже начал искать их повсюду.
Напомним, что треугольник называется прямоугольным, если градусная мера одного из его углов равна 90 градусам.
Однажды Петр увидел на классной доске n точек и заинтересовался количеством троек из этих точек, на которых можно построить прямоугольные треугольники. Помогите удовлетворить его интерес.
Технические условия.
Программа читает со стандартного входа (клавиатуры) целое число n (3≤ n ≤1000) и n пар целых чисел - xi и yi — координаты i-ой точки. Координаты точек не превышают 30000 по абсолютной величине. Все точки различны.
Программа выводит на стандартный выход (экран) количество троек точек, на которых можно построить прямоугольные треугольники.
Пример
Ввод
4 0 0 0 1 2 0 0 -4
Вывод
3
Завдание подготовили B.Боднар, В.Ластовецкий, Г.Непомнящий, Ю.Пасихов, І. Порублев


