Задача Like3
Назвемо натуральне число триподібним (тобто, подібним числу 3), якщо його запис містить лише ті цифри, котрі можна подати у вигляді степеня (з цілим показником) числа 3. Знайдіть кількість триподібних чисел, що належать проміжку [A; B].
Технічні умови: Програма Like3 повинна прочитати з пристрою стандартного введення (клавіатури) числа A і B , записані в один рядок через пропуск (1<= A <= B <=1039 ).
Програма повинна вивести на пристрій стандартного виведення (екран) єдине число – шукану кількість триподібних чисел.
Приклади:
Введення: 1 10
Виведення: 3
Введення 11 94
Виведення 8
Задача DDR3
На заводі, що виробляє модулі пам’яті DDR3, облік виготовленої за добу продукції ведеться автоматично: комп’ютер послідовно записує номери виготовлених модулів, нумерючи їх від 1 послідовним рядом чисел, до останнього за цю добу. Але через помилку програміста відбувся збій. Замість послідовності номерів, що йдуть підряд, програма видала послідовність довжиною К цифр без пропусків, та й ще, якщо у цій послідовності повинно було бути кілька однакових цифр підряд, друкувала одну. Програміста, звичайно, викликали на «килим». Допоможіть йому швидко відповісти на питання, скільки модулів було випущено за добу? Майте на увазі: інших помилок (крім загублених при друці кількох підряд однакових цифр та заміни їх однією та загублених пропусків) в програмі не було.
Технічні умови: Програма DDR3 читає із пристрою стандартного введення одне число К (1<=K<=1018). Програма виводить на пристрій стандартного виведення єдине число – кількість виготовлених за добу модулів.
Приклад
Введення 13
Виведення 12
При правильно працюючій системі обліку повинно бути
1 2 3 4 5 6 7 8 9 10 11 12
Програма видала
1234567891012, тобто 13 цифр без пропусків.Задача Tourist
Туристу набридло подорожувати уздовж координатної вісі, тому він вирішив помандрувати ще по координатній площині. Він розпочинає зі своєї бази в точці A 1 з координатами x 1 y 1 , рухається найкоротшим маршрутом до визначної пам’ятки A 2 з координатами x 2y 2 , далі, не зупиняючись, рухається найкоротшим маршрутом до визначної пам’ятки A3 з координатами x 3 y3, і так далі. Дійшовши до останньої визначної пам’ятки An з координатами xnyn , він, не зупиняючись, рухається до своєї бази. Турист вважає свій маршрут неприємним, якщо існує така пряма, що він уздовж неї не рухався, і разом з тим перетинав її строго більше двох разів. Якщо маршрут не є неприємним, турист вважає його приємним.
Турист вважає, що перетинав пряму, якщо в деякий момент часу перебував у одній півплощині відносно неї, а через деякий дуже малий проміжок часу — в іншій півплощині (сама пряма не належить жодній з півплощин).
Напишіть програму, яка, прочитавши описи кількох маршрутів, визначить, чи приємний кожен з них.
Програма повинна прочитати зі стандартного входу (клавіатури) спочатку кількість маршрутів K (2<=K<=12), потім K однотипних блоків, кожен з яких описує маршрут. Кожен блок опису маршруту починається числом n (2<=n<=98765), далі йдуть n пар цілих чисел, що не перевищують 108 за абсолютною величиною — координати x1 y1 x2 y2… xn yn. Всі числа всіх маршрутів записані в одному рядку й розділені одинарними пробілами. Сумарна кількість всіх вершин усіх маршрутів, які програма має обробити за один запуск, не перевищуватиме 123456.
Програма повинна вивести на стандартний вихід (екран) у один рядок K розділених пробілами нулів та/або одиниць, які позначають, приємними (1) чи неприємними (0) були відповідні маршрути.
Приклад
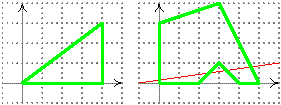
Вхід: 2 3 0 0 4 0 4 3 7 0 3 0 0 2 0 3 1 4 0 5 0 3 4
Вихід: 1 0
Задача Dividers
Знайдіть максимальну кількість натуральних дільників серед усіх натуральних чисел в діапазоні від 1 до N (1<=N<=1019), обидві межі включно).
Технічні умови.Програма читає з пристрою стандартного введення (клавіатури) натуральне число N (1<=N<=1019. Програма виводить на екран єдине натуральне число — максимальну кількість натуральних дільників для всіх чисел від 1 до N.
Приклад
Введення
42
Виведення
9
Пояснення. Серед усіх чисел від 1 до 42, число 36 має 9 дільників (перелік: 1, 2, 3, 4, 6, 9, 12, 18, 36), а всі інші — меншу кількість дільників.
Задача Railway
В країні Олімпія трапилась економічна криза. Не оминуло це і місцеву залізницю. Після останніх реформ залізниця Олімпії стала складатись з N станцій та N-1 перегонів, які з'єднують ці станції. Кожна станція може бути безпосередньо з'єднана не більше, ніж з шістьма іншими станціями. Між будь-якою парою різних станцій існує лише один спосіб дістатися від першої станції до другої.
Найбільших проблем залізниця Олімпії зазнає від розкрадачів, які вночі знімають рейки з залізничних колій. Злодії можуть починати свій рух з будь-якої станції та безперешкодно прямувати до будь-якої іншої станції, рухаючись лише по колії, а потяги в Олімії ночами не ходять - шлях вільний. Але злодіїї не можуть проїжджати одну станцію більше, ніж один раз - бояться.
Дирекція залізниці просить вас визначити найбільший збиток та кількість способів його спричинити.
Технічні умови: Програма повинна прочитати з клавіатури натуральне число N (1 <= N <= 100000) -- кількість залізничних станцій, а потім N-1 трійок натуральних чисел. Кожна трійка містить інформацію про один перегін. Перші два числа - номери станцій, які з'єднує даний перегін, третє число - довжина перегону в кілометрах (довжина не може перевищувати 1000 км).
Програма повинна виводити на екран два числа через пробіл - найбільш можливий збиток (сумарна довжина колій, які розкрадачі можуть розібрати) та кількість способів його спричинити.
Приклади:
Введення: 3 1 2 1 2 3 2
Виведення: 3 2
Введення: 5 1 2 1 1 3 1 1 4 1 1 5 1
Виведення: 2 12


