Решения принимаются до 0 часов 03.02.12
Задача Like3
Назовем натуральное число триподобным (то есть, подобным числу 3), если его запись содержит только те цифры, которые можно представить в виде степени (с целым показателем) числа 3. Найдите количество триподобных чисел, которые принадлежат промежутку [A; B].
Технические условия: Программа Like3 должна прочитать с устройства стандартного ввода (клавиатуры) числа A и B, записанные в одну строчку через пробел (1<=A<=B<=1039).
Программа должна вывести на устройство стандартного вывода (экран) единственное число – искомое количество триподобных чисел.
Примеры:
Ввод: 1 10
Вывод: 3
Ввод: 11 94
Вывод: 8
Задача DDR3
На заводе, который изготовляет модули памяти DDR3, учет изготовленной за день продукции ведется автоматически: компьютер последовательно записывает номера изготовленных модулей, нумеруя их от 1 последовательным рядом чисел, до последнего за эти сутки. Но из-за ошибки программиста произошел сбой. Вместо последовательности номеров, идущих подряд, программа выдала последовательность длиной К цифр без пробелов, кроме всего прочего, если в этой последовательности должно было быть несколько одинаковых цифр подряд, печатала одну.
Программиста, конечно же, вызвали на «ковер». Помогите ему быстро ответить на вопрос, сколько модулей было выпущено за сутки? Имейте в виду: других ошибок (кроме потерянных при печати нескольких подряд одинаковых цифр и замене их одной, а также потерянных пробелов) в программе не было.
Технические условия: Программа DDR3 читает с устройства стандартного ввода одно число К (1<=K<=1018). Программа должна вывести на устройство стандартного вывода единственное число – количество изготовленных за сутки модулей.
Пример
Ввод: 13
Вывод: 12
Разъяснение.
При правильно работающей системе учета должно быть
1 2 3 4 5 6 7 8 9 10 11 12
Программа выдала 1234567891012, то есть 13 цифр без пробелов.
Задача Tourist
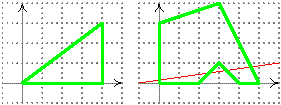
Турист полагает, что пересекал прямую, если в один момент времени находился в одной полуплоскости относительно нее, а через некоторый очень малый промежуток времени – в другой полуплоскости (пересекаемая прямая не принадлежит ни одной из полуплоскостей).
Напишите программу, которая, прочитав описания нескольких маршрутов, определит, приятен ли каждый из них.
Программа должна прочитать со стандартного входа (клавиатуры) сначала количество маршрутов K (2<=K<=12), потом K однотипных блоков, каждый из которых описывает маршрут. Каждый блок описания маршрута начинается числом n (2<=n<=98765), дальше записано n пар целіх чисел, не превосходящих 108 по абсолютной величине — координаты x1 y1 x2 y2 … xn yn. Все числа всех маршрутов записаны в одной строке и разделены одинарными пробелами. Суммарное количество всех вершин всех маршрутов, которые программа должна обработать за один запуск, не превышает 123456.
Программа должна вывести на стандартный выход (экран) в одну строку K разделенных пробелами нулей и/или единиц, которые обозначают, приятными (1) или неприятными (0) были соответственные маршруты.
Пример
Ввод: 2 3 0 0 4 0 4 3 7 0 3 0 0 2 0 3 1 4 0 5 0 3 4
Вывод: 1 0
Задача Dividers
Найдите максимальное количество натуральных делителей среди всех натуральных чисел диапазона от 1 до N (1<=N<=1019, обе границы включительно).
Технические условия Программа читает с устройства стандартного ввода (клавиатуры) натуральное число N (1<=N<=1019). Программа выводит на экран единственное натуральное число — максимальное количество натуральных делителей для всех чисел от 1 до N.
Пример
Ввод: 42
Вывод: 9
Разъяснение. Среди всей чисел от 1 до 42, число 36 имеет 9 делителей (перечень: 1, 2, 3, 4, 6, 9, 12, 18, 36), все же другие — меньшее количество делителей.
Задача Railway
В стране Олимпия произошел экономический кризис. Не обошел он и местную железную дорогу. После очередных реформ железная дорога состоит из N станций и N-1 перегонов, которые соединяют эти станции. Каждая станция может быть непосредственно соединена не более, чем с шестью другими станциями. Между любой парой разных станций существует только один способ добраться от первой станции до второй.
Наибольшие проблемы железной дороге Олимпии причиняют расхитители, которые ночью снимают с железнодорожных путей рельсы. Воры могут начинать свое движение с любой станции и беспрепятственно двигаться к любой другой станции по рельсам (благо поезда ночами не ходят - путь свободен). При этом никакую станцию им нельзя проезжать больше одного раза - могут засечь.
Дирекция железной дороги просит Вас определить наибольший ущерб и количество способов, которыми он может быть причинен.
Технические условия: Программа должна прочитать с клавиатуры натуральное число N (1 <= N <= 100000) – количество железнодорожных станций, а потом N-1 тройку натуральных чисел. Каждая тройка содержит информацию об одном перегоне. Первые два числа тройки – номера станций, которые соединены этим перегоном, третье число – длина перегона в километрах (длина не может превышать 1000 км).
Программа должна вывести на экран два числа через пробел – наибольший ущерб (суммарная длина путей, которые расхитители могут разобрать) и количество способов, которыми он может быть причинен.
Примеры:
Ввод: 3 1 2 1 2 3 2
Вывод: 3 2
Ввод: 5 1 2 1 1 3 1 1 4 1 1 5 1
Вывод: 2 12


