Задача HardWay. Не «ведіться» на назву задачі. Навпаки, на цьому тест-драйві водієві нового позашляховика доведеться їхати зовсім не по твердому покриттю, а навпаки, по рівнині, яка покрита піском. Вся рівнина розбита паралельними осі Х прямими на своєрідні полоси-зони. В межах кожної зони однорідний, але різний для кожної зони шар піску. Відповідно для кожної полоси є реально досяжна двигуну максимально дозволена швидкість руху. Зрозуміло, що N - 1 горизонтальна пряма задає розмежування N таких зон. Крім того, задані координати початкового і кінцевого пунктів маршруту.
Вам необхідно знайти мінімальний можливий час тест-драйву.
Технічні умови Програма HardWay читає з пристрою стандартного введення у першому рядку число N (2 ≤ N ≤ 30) - кількість зон на мапі. З наступного рядка програма читає N - 1 число yi, що задають прямі y = yi - межі зон (i-та пряма задає межу між i та i+1 зонами). З третього рядка програма читає чотири числа xA yA xB yB - координати початкової і кінцевої точок маршруту. Усі числа натуральні і задовольняють нерівність: 0 < yA < y1 < y2 < … < yN-1 < yB ≤ 100’000, xA ≤ 100’000, xB ≤ 100’000. З четвертого рядка програма читає N чисел Vi – максимально можливі швидкості у кожній з N зон. При цьому 1 ≤ Vi ≤ 10000. Швидкості подано у порядку подолання зон.
Програма виводить рівно одне дійсне число - мінімальний час, необхідний на шлях між пунктами A та B за умови руху по кожній зоні з максимально можливій для неї швидкості. Відповідь буде зараховано, якщо абсолютна чи відносна похибки складуть не більш як 10-6.
Приклади
|
Введення |
Виведення |
Коментар |
|
|
2 2 1 1 1 22 1 20 |
2.0000000 |
Оптимальним буде рух по прямій - тоді у першій зоні буде подолано 1 одиницю шляху (зі швидкістю 1), у другій 20 одиниць (зі швидкістю 20), усього 2 одиниці часу. |
|
|
3 5 11 1 1 15 15 3 4 3 |
5.8333333 |
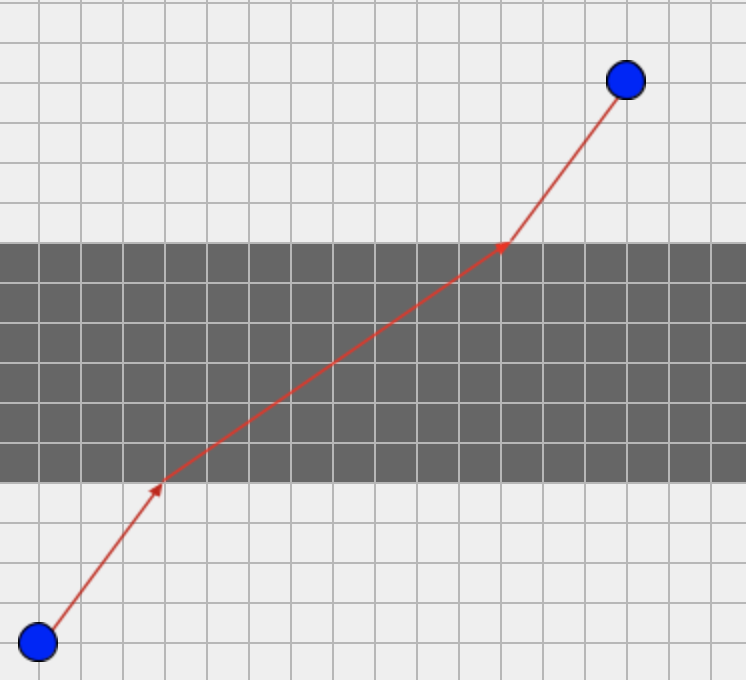
Відображено (див.малюнок) оптимальний маршрут. Витрачений час при цьому складе 5/3 + 10/4 + 5/3 = 35/6, тобто 5,8(3) |
|