Задания по информатике
Командный тур
Задача Сопротивление (RESIST)
К резистору с сопротивлением R1 последовательно подключается резистор с сопротивлением R2. Затем к полученной схеме подключается параллельно резистор с сопротивлением R1. Далее опять подключается резистор с сопротивлением R2 и т.д. Всего в схеме будет N резисторов. (см. рисунок).
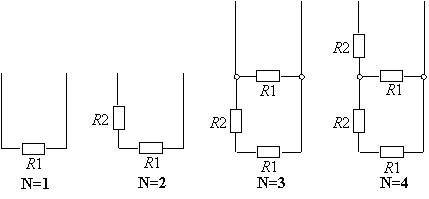
Определите, какое сопротивление будет иметь такая схема.
Формат ввода/вывода:
Напишите программу RESIST, которая читает три целых числа N, R1, R2. Программа должна вывести сопротивление всей схемы с точностью не меньше, чем 10−10.
Ограничения: . 1≤N≤2 147 483 647, 1≤R1,R2≤5000.
Пример:
|
Ввод 4 1 1 |
Вывод 1.666666667 |
Задача Ленточка (RIBBON)
Есть ленточка, на которой может быть записано натуральное число, состоящее ровно из N цифр. Над ленточкой можно выполнить следующую операцию: разрезать ленточку между любыми двумя последовательными цифрами числа, не переворачивая, поменять местами получившиеся два куска, и склеить их снова. Ленточка считается красивой, если после этой операции на склеенной ленточке окажется то же самое число. Например, ленточка с числом 5656 является красивой, а 5665 – нет. Требуется найти количество различных чисел, которые при записи на ленточке делают ее красивой.
Формат ввода/вывода:
Напишите программу RIBBON, которая считывает одно целое число: длину ленточки N. Необходимо вывести количество N-значных чисел, делающих ленточку красивой, по модулю 1 000 007.
Ограничения: 1≤N≤1 000 007.
Пример:
|
Ввод 4 |
Вывод 90 |
Задача Резервуар (VESSEL)
Рассмотрим ломаную, координаты вершин которой (x1, y1), (x2, y2), (x3, y3), …, (xN, yN) удовлетворяют неравенствам xi < xi+1 и yi ≠ yi+1 для всех i. Проведем лучи вертикально вверх из крайней левой (x1, y1) и крайней правой (xN, yN) вершин. Потом превратим плоскую фигуру в трехмерное тело, имеющее в направлении оси Oz постоянную толщину 1.
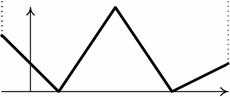 Þ
Þ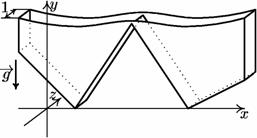
Согласно этим правилам изготовили резервуар: его передняя и задняя стенки – плоские, вертикальные, параллельные друг другу (расстояние между ними – 1), левая и правая стенки (полученные из вертикальных лучей) также плоские, вертикальные и параллельные друг другу. Ломаная задает форму дна. Резервуар неподвижно закреплен, поэтому независимо от формы дна и от наполнения он не будет опрокидываться.
В этот резервуар вдоль его левой стенки постепенно наливают воду. Всего налито V кубических единиц воды. Требуется вычислить площадь полученной водной поверхности. (Поверхностными явлениями пренебречь).
Формат ввода/вывода:
Напишите программу VESSEL, которая считывает два целых числа – количество вершин ломаной N и объем воды V, а затем N пар целых чисел – координаты (в порядке x1 y1 x2 y2 … xN yN). Необходимо вывести площадь водной поверхности с точностью не менее 10−3.
Ограничения: 2 ≤ N ≤ 12 345, 0 ≤ V ≤ 1012, координаты не превышают по модулю 106.
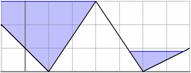
Пример:
|
Ввод 5 8 -1 2 1 0 3 3 5 0 7 1 |
Вывод 6.309401 |


