Завдання для учнів 9-11 класів
Час виконання – 5 годин
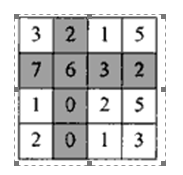
Задача Table2021 Дано прямокутну таблицю А розміром nxn (1≤n≤100), що заповнена цілими числами.(-65000≤Ai,j≤65000) Потрібно отримати прямокутну таблицю B розміром nxn, кожний елемент якої (bi,j) i,j=1,2,…n рівний максимальному елементу в i-му рядку та j-му стовпчику таблиці А
Технічні умови. Програма Table2021 читає з пристрою стандартного введення в першому рядку число n, а далі n рядків по n чисел в кожному – елементи таблиці А. Числа в рядках відокремлені пропусками. Програма виводить на пристрій стандартного введення – n рядків та n стовбців масиву B. Числа в рядках розділені пропусками.
Приклад
|
Введення 4 3 2 1 5 7 6 3 2 1 0 2 5 2 0 1 3 |
Виведення
7 6 5 5 7 7 7 7 7 6 5 5 7 6 3 5 |
Задача Time2021. При авіаційному сполученні використовують місцевий час аеропортів вильоту та прибуття. Часові пояси характеризуються різницею в часі з меридіаном, на якому знаходиться Грінвічська обсерваторія. Для кожного часового поясу вводиться відхилення від UTC (Всесвітній координований час). Наприклад, місто аеропорт А знаходитися в часовому поясі UTC+3, а аеропорт В - UTC+7. Якщо рейс з А в В триває рівно 4 години, літак з А вилетів о 11:15, то в В він прибуде о 19:15 (4 годин польоту+4 години різниця в часі). Часові пояси змінюються від UTC-11 до UTC+14. По заданому часу вильоту та часу польоту, а також по годинним поясам аеропортів вильоту та прибуття треба визначити місцевий час прильоту та кількість днів, проведених в польоті.
Технічні умови. Програма Time2021 читає з пристрою стандартного введення в першому рядку 2 числа через пропуск HD, MD (0 ≤ HD ≤ 23, 0 ≤ MD ≤ 59) – час вильоту, в другому рядку HF , MF (0 ≤HF ≤ 109 , 0 ≤ MF ≤ 59) – час польоту, в третьому рядку 2 цілих числа D, A (−11 ≤ D, A ≤ 14) - часові пояси аеропортів вильоту та прильоту. Програма виводить на пристрій стандартного виведення три числа в одному рядку через пропуски HA, MA, Days час прильоту в годинах та хвилинах, а різницю в датах вильоту та прильоту.
Приклади
|
Введення |
Виведення |
Коментар |
|
11 15 4 0 3 7
|
19 15 0 |
Відповідає прикладу в задачі |
|
12 0 1 0 -10 13 |
14 0 1 |
В цьому прикладі літак перетнув лінію зміни дати |
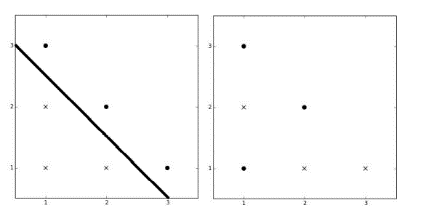Задача learning. У машинному навчанні часто виникає завдання лінійної класифікації об'єктів, коли класи об'єктів поділяються між собою лінійною поверхнею. Наприклад, у нас є інформація про кількість днів з моменту реєстрації облікового запису в соціальній мережі та кількість надісланих повідомлень за останній день, а також інформація про те, чи є цей обліковий запис спам-ботом. Вік облікового запису ми можемо взяти за X координату точки, а кількість повідомлень за Y координату. Завдання класифікації полягає в тому, щоб провести якусь пряму так, щоб об'єкти одного тину знаходилися по одну сторону цієї прямої, а об'єкти іншого тину та іншу.
За наявності такої прямої ми зможемо прогнозувати тип навіть незнайомого об'єкта але відомому віку облікового запису та кількості відправлених повідомлень залежно від того, з якого боку від прямої виявився об'єкт. Звичайно, у реальних даних можуть бути помилки вимірів або незвичайні об'єкти і провести таку пряму не всіх так можливо, тому що, наприклад, об'єкт першого тину може випадково потрапити в скупчення об'єктів другого типу і відокремити його прямо неможливо.
Вам необхідно за інформацією про параметри та тип об'єктів визначити, чи існує пряма, яка однозначно поділяє класи об'єктів. Пряма не повинна проходити ні через один об'єкт.
Технічні умови. Програма Learning читає з пристрою стандартного введення кілька тестових блоків. У першому рядку задано число Т - кількість тестових блоків (1 ≤ Т ≤ 100). Кожен тестовий блок складається з числа N - кількість описаних об'єктів (1 ≤ N ≤ 2000). У наступних N рядках міститься опис об'єктів, що складаються з трьох цілих чисел X, У, Туре (0 < X, У < 107, 0 ≤ Туpe ≤ 1). Програма виводить на пристрій стандартного виведення для кожного тестового блоку YES, якщо поділ можливий і NO, якщо ні, для кожного блоку в окремій стрічці.
Приклад
|
Введення |
Виведення |
|||
|
2 |
|
|
|
YES |
|
6 |
|
|
|
NO |
|
1 |
1 |
1 |
|
|
|
1 |
2 |
1 |
|
|
|
1 |
3 |
0 |
|
|
|
2 |
1 |
1 |
|
|
|
2 |
2 |
0 |
|
|
|
3 |
1 |
0 |
|
|
|
6 |
|
|
|
|
|
1 |
3 |
0 |
|
|
|
2 |
2 |
0 |
|
|
|
1 |
2 |
1 |
|
|
|
3 |
1 |
1 |
|
|
|
2 |
1 |
1 |
|
|
|
1 |
1 |
0 |
|
|
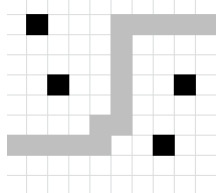
Задача Toxins. У популярній настільній грі завдання полягає в тому, щоб провести фішку по певному маршруту. Поле є прямокутником, що складається з квадратних клітинок. Гравець може за один хід перейти в одну з чотирьох сусідніх по стороні клітинок, не виходячи при цьому за межі поля. Гравець починає свій шлях у будь-якій клітинці самого лівого стовпця і повинен потрапити до будь-якої клітинки самого правого стовпця ігрового поля.
Але окремі клітинки токсичні, їх розташування відоме. Вася з'ясував, що чим більша відстань від токсичної клітинки, тим безпечніший маршрут, відстань обраховується як кількість ходів клітинками токсичних клітинок до кожної клітинки маршруту. Допоможіть йому визначити, на яку мінімальну відстань доведеться підійти до токсичної клітинки, рухаючись найбезпечнішим маршрутом.
Технічні умови. Програма Toxins читає з пристрою стандартного введення першому рядку записано натуральні числа N та М (1 ≤ N,М ≤500) — кількість рядків та стовпців на ігровому полі, у другому рядку записано натуральне число К (1≤К≤500) — кількість токсичних клітинок. У наступних К рядок записані пари чисел Ri Ci (1≤ Ri ≤N, 1≤Ci≤ М) — координати токсичних клітинок (рядок, стовпець). Програма виводить на пристрій стандартного виведення мінімальну відстань, на яку доведеться наближатися до токсичної клітинки на безпечному маршруті.
Приклад
|
Введення |
Виведення |
Коментар |
|
10 10 4 2 2 5 3 5 9 8 8
|
3 |
Приклад одного з безпечних маршрутів показано на малюнку. Токсичні клітинки – чорні, клітинки маршруту – сірі. Мінімальна відстань між токсичною клітинкою та маршрутом – 3 ходи |
