Розв'язки приймаються до 0 годин 12 лютого 2020 р.
==============================================
Задача Train2020. Укрзалізниця активно розширює міжнародне сполучення. Для збільшення кількості маршрутів було придбано надсучасні поїзди класу Інтерсіті++. Пробна серія включала рівно один локомотив (з номером 1) та N-1 вагон з номерами від 2 до N.
Після придбання було виявлено, що особливості будови механізму зчеплення вагонів дозволяють зчіплювати лише ті вагони, номери яких мають спільний дільник, відмінний від одиниці. Виключення стосується лише локомотива - він може бути причеплений лише попереду потяга і має можливість зчепитися з будь-яким вагоном.
Від кількості вагонів у рухомому складі залежить прибуток компанії, а тому керівництво просить вас про допомогу - визначити максимальну кількість вагонів (з урахуванням локомотива), які можна сполучити послідовно у рухомий склад.
Технічні умови Програма Train2020 зчитує з пристрою стандартного введення єдине число N - кількість отриманих вагонів (N≤105). Програма повинна виводити рівно одне число - максимальну довжину рухомого складу.
Приклади
|
Введення |
Виведення |
Коментар |
|
3 |
2 |
Вагони 2 та 3 сполучити не можна, а тому рухомий склад буде або 1-2, або ж 1-3 |
|
6 |
5 |
Можливий варіант рухомого складу наступний: 1-2-4-6-3 |
Задача Game2020. Улюблена справа колядників - ділити зароблені солодощі та гроші. Олесь та Михась отримали купу цукерок, а крім того грошову купюру певного номіналу. Звісно що ця купюра представляє для хлопців найбільший інтерес, а дорослих, які б могли розміняти суму порівно, немає. Тому старшим братом було запропоновано зіграти у наступну гру.
Кожному з гравців по черзі доводиться обирати деякий непорожній набір кошиків з ряду (таких, що стоять поруч), а далі з кожного необхідно забрати щонайменше по одній цукерці. Такі дії гравці роблять, поки у когось не залишиться можливості зробити хід - тоді цей гравець програє і гроші дістаються переможцю.
Михась вже розклав цукерки по кошикам, але Олесь підозрює, що брат заздалегідь точно знає, що зможе виграти. Олесь, як молодший брат, ходить першим і просить у вас допомоги - чи зможе має він деяку виграшну стратегію для заданого набору цукерок?
Технічні умови З першого рядку стандартного пристрою введення програма Game2020 зчитує єдине число T (1 ≤ T ≤ 10) - кількість тестів. Далі, у T парах рядків слідують вхідні дані у вигляді:
- У першому в парі - число N (1 ≤ N ≤ 106) - кількість кошиків з цукерками
- У другому в парі - N чисел Ai (0 ≤ Ai ≤ 105) - кількість цукерок у кошиках
Програма має вивести рядок з рівно N символів - відповіді на кожен з тестів у тій самій послідовності, що і у вхідних даних. Програма має вивести Y, якщо у Михась точно має стратегію для перемоги і N у іншому випадку.
Приклади
|
Введення |
Виведення |
Коментар |
|
3 3 1 0 1 4 1 5 6 1 5 1 0 1 1 1 |
YNN |
У першому випадку Олесь має опорожнити один з кошиків, після чого Михась забере цукерку з іншого і виграє. У другому випадку Олесь може забрати усі цукерки одразу, чим забезпечить перемогу. У третьому випадку Олесь може опорожнити два з трьох кошиків, що йдуть підряд, після чого Михасю доведеться взяти цукерку з одного з кошиків, що залишились, що дасть перемогу Олесю. |
Задача Wall2020
На ідеально гладенькій горизонтальній поверхні нерухомо стоїть куб з масою m1. Неподалік від кубу височіє, стіна, площина якої паралельна одній з бокових граней куба. З протилежного від стіни боку з деякою швидкістю ковзає у напрямку стіни куб з масою m2,. Швидкість перпендикулярна до стіни та бокових граней обох кубів Усі удари абсолютно пружні. Зрозуміло, що після зіткнення перший куб почне ковзати у напрямку стіни, після чого відіб’ється. і, вірогідно, ще раз стикнеться з другим. Вам потрібно визначити загальну кількість зіткнень, що відбудуться в системі.
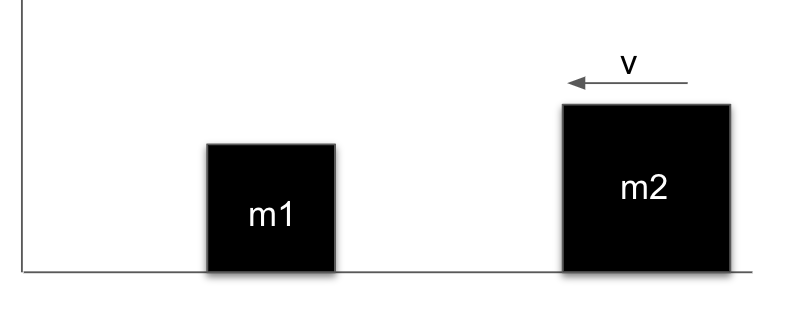
Технічні умови. Програма Wall2020 читає з пристрою стандартного введення два цілих числа m1 та m2 - маси кубів (1 ≤ m1 ≤ m2 ≤ 103). Програма має виводити єдине ціле число - кількість ударів.
|
Введення |
Виведення |
Коментар для тих, хто не має часу вивчати шкільну фізику |
|
1 10 |
10 |
Абсолютно пружний удар – взаємодія тіл без втрат ними сумарної механічної енергії |
|
10 10 |
3 |
Задача Trunks. Скрудж Макдак знайшов печеру, де в один ряд стояли скрині. На стіні печери написано:
- З першої скрині можна взяти рівно K монет;
- З кожноі наступної скрині можна взяти довільну кількість монет, але хоча б одну;
- Не можна брати з наступної скрині стільки ж монет, що і з попередньої;
- Якщо з чергової (останньої на цей час) скрині взяти менше монет, ніж з передостанньої, то з наступної треба взяти більше, ніж з останньої;
- Якщо з останньої скрині взяти більше монет, ніж з передостанньої, то з наступної треба взяти менше, ніж з останньої;
- Загалом можна взяти рівно N монет.
Допоможіть Скруджу підрахувати, скількома способами він зможе винести з печери монети. Вважайте, що скринь, а також монет у кожній скрині достатньо.
Технічні умови. Програма Trunks читає з пристрою стандартного введення числа N і K (1≤N≤5000, 1≤K≤N) і виводить на пристрій стандартного виведення остачу при ділення шуканої кількості на 109+7.
Приклади
Введення 3 3
Виведення 1
Введення 6 2
Виведення 4
Пояснення. Для другого прикладу можливі способи: [2,1,2,1], [2,1,3], [2,3,1], [2,4].
Задача Kingdoms2020. Автори казок знають, що є ще царства окрім Тридев'ятого, і вони характеризуються як (N,K) - Царства. Але існувати (N,K) - Царство може лише тоді, коли K може бути представлено у вигляді суми не більше ніж N простих чисел.
Наприклад, (3,9) - (Тридев’яте) Царство існує, тому що 9 = 2 + 7 (ще варіанти: 9 = 3 + 3 + 3 і 9 = 2 + 2 + 5). Також має право на існування і (2,10)- (Двадесяте) Царство, так як 10 = 5 + 5. У той же час (2,27)-е (Двадвадцатьсьоме) Царство існувати не може, оскільки 27 неможливо представити у вигляді суми не більше чим двох простих чисел.
Знайдіть кількість існуючих (N, K)-царств за умови, що числа N і K можуть змінюватися в деякому діапазоні: a ≤ N ≤ b, c ≤ K ≤ d.
Технічні умови. Програма Kingdoms2020 читає з пристрою стандартного введення чотири цілі числа в одному рядку через пропуски: a і b - нижнє і верхнє обмеження на N. Та цілі числа c і d - нижнє і верхнє обмеження на K. Програма виводить на пристрій стандартного виведення єдине число, рівне кількості існуючих (N, K)-царств, для яких a ≤ N ≤ b і c ≤ K ≤ d. Розмір тексту розв’язку не повинен бути більшим 16 Кб.
Обмеження:
1. Число a від 1 до 1000000 включно.
2. Число b від a до a + 1000 включно.
3. Число c від 1 до 1000000 включно.
4. Число d від c до c + 1 000 включно.
Приклади
|
Введення |
Виведення |
Коментарі |
|
1 1 2 10 |
4 |
У цьому прикладі нам необхідно знайти числа K, які представляються у вигляді суми не більше 1-го простого числа, тобто є простими. На відрізку від 2 до 10 включно є 4 простих числа - 2, 3, 5 і 7. |
|
1 2 20 30 |
12 |
(N, K)-царства існують:
Всього маємо 2 + 10 = 12 царств. |
|
2 4 45 64 |
58 |
|
|
1 20 469588 470425 |
15701 |
|
Додаткова інформація
Цитата з однієї, дуже відомої, «казки»: «Натуральне число X, більше одиниці, називається простим, якщо воно не ділиться без остачі ні на які числа, окрім 1 і X.»
Завдання підготували Зуєв А, В.Мельник, Г.Непомнящий, М.Стречень, Ю.Пасіхов


