Завдання з інформатики
Командний тур
Задача Бульбашки (BUBBLES)
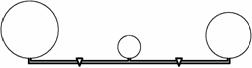 Як відомо, коли дві бульбашки різного діаметру з’єднані трубкою, менша з них зменшується (а більша зільшується), доки менша не стане нульового розміру. Будемо вважати, що сумарний об’єм бульбашок при цьому зберігається.
Як відомо, коли дві бульбашки різного діаметру з’єднані трубкою, менша з них зменшується (а більша зільшується), доки менша не стане нульового розміру. Будемо вважати, що сумарний об’єм бульбашок при цьому зберігається.
Існує конструкція, де 1‑а та 2‑а бульбашки, а також 2‑а та 3‑я з’єднані трубками з кранами. Це дає можливість дозволяти/забороняти природнє перетікання газу окремо між 1‑ою і 2‑ою бульбашками, і окремо між 2‑ою і 3‑ою. Можна частково відкрити кран і закрити у потрібний момент, щоб відбулося перетікання визначеного об’єму газа.
Потрібно з’ясувати, чи можна досягти того, щоб 1‑а та 3‑я бульбашки стали однакового розміру.
Технічні умови. Програма BUBBLES читає з клавіатури три рядки по три числа V1, V2, V3 у кожному. Кожен рядок є окремим прикладом, для якого потрібно вивести на екран у окремому рядку або число 1 (якщо можливо отримати рівність крайніх бульбашок), або 0 (якщо ні). Усі об’єми – цілі додатні числа, що не перевищують 1000.
Приклад
|
Введення |
Виведення |
|
4 1 1 41 2 41 17 42 9 |
0 1 1 |
Задача Майже арифметична прогресія (ARITHM)
Послідовність чисел називається «майже арифметичною», якщо модуль різниці між будь-якими двома її сусідніми елементами однаковий. Потрібно для заданої послідовністі визначити, чи можна переставити її елементи таким чином, щоб вона стала «майже арифметичною».
Технічні умови. Програма ARITHM читає з клавіатури ціле число N (1≤N≤200000) — кількість елементів у послідовності, а у другому – саму послідовність. Усі числа послідовності не перевищують 106 по модулю. Програма виводить на екран N чисел, які ви значають «майже арифметичну» послідовність, що отримується з вхідної перестановкою її елементів. Якщо такої перестановки не існує, виведіть повідомлення «No solution» без лапок.
Приклад
|
Уведення |
Виведення |
|
5 4 3 3 2 4 |
4 3 4 3 2 |
|
3 10 20 40 |
No solution |
Задача Триангуляція (TRIANG)
Триангуляцією опуклого многокутника називається розбиття його на трикутники діагоналями, що попарно не перетинаються. Степінню вершини відносно заданої триангуляції будемо вважати кількість діагоналей, які виходять з цієї вершини.
Дано правильний N-кутник. Перенумеруємо всі його вершини у порядку обходу проти годинникової стрілки натуральними числами від 1 до N. Нехай дано невід’ємні цілі числа d1, d2, …, dN. Потрібно визначити, чи існує хоча б одна така триангуляція, що для усіх i від 1 до N вершина i має відносно неї степінь di, і якщо існує, вказати будь-яку з них.
Технічні умови. Програма TRIANG у першому рядку читає з клавіатури ціле число N (3≤N≤200000), у другому – N цілих чисел d1, d2, …, dN (0≤di≤N). Програма виводить на екран К – кількість діагоналей, які задають шукану тріангуляцію, а далі – K рядків з діагоналями. Кожна діагональ задаєтся двома числами – номерами вершин, які нею з’єднуються. Кожна діагональ повинна виводитися у окремому рядку. Номери вершин розділяються одним пропуском. У випадку, якщо триангуляції із заданими степенями вершин не існує, виведіть одне число -1.
Приклад
|
Уведення |
Виведення |
|
6 1 0 2 1 0 2 |
3 1 3 3 6 4 6 |
|
5 2 0 2 0 2 |
-1 |


