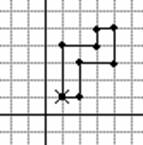
Задача Division
Напишите программу, находящую для натуральных чисел A, B и k различных простых чисел количество чисел в диапазоне от A (включительно) до B (включительно), которые не делятся ни на одно из заданных простых чисел.
Технические условия. Программа Division читает с клавиатуры в одной строке сначала числа A, B (1 ≤ A < B ≤ 1018), затем количество простых чисел k (1 ≤ k ≤ 100), затем k штук различных простых чисел, каждое из которых не больше 1018.
Программа выводит на экран единственное целое неотрицательное число — количество чисел в диапазоне от A до B включительно, которые не делятся ни на одно из заданных простых чисел.
Приклад
Ввод
17 42 3 2 3 5
Вывод
7
Пояснения к примеру. Числами в диапазоне от 17 до 42, которые не делятся ни на 2, ни на 3, ни на 5, являются числа 17, 19, 23, 29, 31, 37 та 41. Их 7 штук.
Задача Prize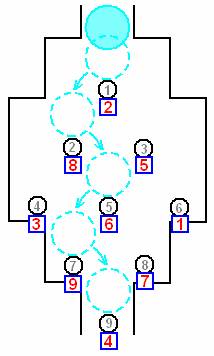 
Для розыгрыша денежных призов использовали игровой аппарат, конструкция которого состоит из вертикально размещенного плоского основания и прикрепленных перпендикулярно к нему N стержней (N – квадрат некоторого натурального числа), пронумерованных от 1 до N (размещение и нумерация стержней показаны на рисунке). Корпус игрового аппарата ограничивает движение шарика так, что его путь обязательно начинается с первого стержня и заканчивается на последнем.
В розыгрыше участвуют ровно N участников, каждый из которых получает свой оригинальный номер (от 1 до N) и перед началом розыгрыша делает ставку, прикрепляя карточку со своим номером к одному из стержней, каждый к своему. Розыгрыш проводят, впуская шарик сверху в игровой аппарат. Стержни, на которые шарик во время свого движения падает вертикально вниз, считаются выигрышными, то есть, выигрышными являются номера участников, сделавших ставку на эти стержни, а сумма выигрыша равна сумме выигрышных номеров участников розыгрыша (см. рисунок).
Во время одного из розыгрышей сумма выигрыша была наибольшей из всех возможных для данных ставок. Найдите эту сумму и номера участников, получивших выигрыш.
Технические условия. Программа Prize читает число N (4≤N≤10000), а в следующей строке N чисел k1, k2, … , kN, де ki – номер участника розыгрыша, сделавшего ставку на i-й стержень. Все числа разделены пробелами.
Программа выводит на экран сумму выигрыша, а далее в следующей строке выигрышные номера участников в порядке возрастания. Все числа разделены пробелами
Пример.
Ввод:
9
2 8 5 3 6 1 9 7 4
Вывод:
29
2 4 6 8 9
В спортивном зале ученики построились в колонну, один за другим. Учитель физкультуры дал команду перестроиться так, чтобы все девочки оказались впереди мальчиков. Какое минимальное количество переходов в другое место колонны должны выполнить ученики? (Переход означает, что ученик или ученица занимает место между двумя другими либо становится в любой конец колонны).
Технические условия. Программа Column читает с клавиатуры число N (1£N£32765) – количество учеников в колонне, а далее N чисел (0 или 1). Все числа разделены пробелами (0 - условное обозначение девочки, 1 - мальчика).
Примеры
Ввод
2 1 0
Вывод
1
Ввод
5 0 0 1 1 1
Вывод
0
Пан Чудак как-то собрал некий капитал (удачно реализовав проект, за который не рискнул взяться никто другой) и решил вложить деньги в бизнес пассажирских перевозок. Он уже выбрал совокупность городов, между которыми хочет организовать сообщение. Крому того, он твердо решил, что последовательности остановок на его маршрутах всегда будут упорядочены по словарным правилам от наименьшего названия до наибольшего («Словарные правила» означает, что при сравнении слов сравниваются сначала первые буквы, если они одинаковы, то вторые, и т. д.). Знакомые убедили его, что это не всегда удобно (например, Винница–Киев–Одесса– Полтава–Симферополь–Ялта). Поэтому сейчас пан Чудак размышляет над компромиссным вариантом: разработать два автобусных маршрута, так, чтобы они имели общее начало (наименьший по словарному порядку город) и конец (наибольший по словарному порядку город), внутри каждого маршрута последовательности городов были упорядочены, и через каждый город проходил хотя бы один из двух маршрутов. Например, для вышеуказанных городов это может быть пара маршрутов Винница–Киев–Полтава–Симферополь–Ялта и Винница–Одесса–Симферополь –Ялта.
Напишите программу, которая поможет пану Чудаку принять решение. Программа должна, прочитав таблицу расстояний между городами, найти длину маршрута, если просто посетить все города по порядку, и минимально возможную суммарную длину пары маршрутов, удовлетворяющей требованиям компромиссного варианта (оба начинаются в первом по словарному порядку городе, заканчиваются в последнем, внутри каждого маршрута все города отсортированы, через каждый город проходит хотя бы один из двух маршрутов).
Технические условия. Программа Towns читает с клавиатуры сначала заданное число N (3 ≤ N ≤ 555), затем N∙(N–1) / 2 чисел, задающих расстояния (от 1‑го города до 2‑го, 3‑го, …, N‑го, затем от 2‑го до 3‑го, …, N‑го, и т. д.). Расстояния натуральны (целые строго положительные) числами, не большими 106. Все числа записаны в одной строке, разделены пробелами. Для расстояний гарантированно выполняется неравенство d(i,j)+d(j,k) ≥d(i,k).
Программа должна вывести на экран через пробел два числа — длину маршрута, который проходит через все города в словарном порядке и минимально возможную суммарную длину компромиссной пары маршрутов.
Пример
Ввод:
5 1 8 6 3 7 5 2 11 7 5
Вывод
24 26
Задача Іnstigator
Маленький мальчик вырезал из бумаги в клеточку многоугольник, причем все разрезы шли по сторонам клеток. Ему интересно, за какое время сгорит многоугольник, если поджечь его в некоторой вершине. Бумага горит равномерно во всех направлениях, и скорость распространения огня равна 1 стороне клетки в секунду. Напишите программу, яка определяет, сколько времени пройдет, прежде чем многоугольник сгорит полностью.
Технические условия.
Программа Іnstigator читает с клавиатуры количество вершин многоугольника N (4<=N<=500), а далее - N пар чисел – координаты вершин в порядке обхода периметра многоугольника. Координаты каждой вершины - два целых числа, не превосходящие по абсолютной величине 10000. Многоугольник поджигается в первой вершине. Описание корректно – стороны многоугольника не имеют общих точек (кроме соседних), каждая вершина соединяет две взаимно перпендикулярные стороны.
Программа выводит одно действительное число – количество секунд, необходимых для полного сгорания многоугольника. Допустима ошибка, не превосходящая 0,001% от правильного ответа.
Примеры
|
Ввод |
Вывод |
|
4 3 0 3 4 0 4 0 0 |
0.500E+01 |
|
Ввод |
Вывод |
|
|
8 1 1 2 1 2 3 4 3 4 5 3 5 3 4 1 4 |
5.064495
|
|
