Задача Newhanoy
Жюри не сомневается в том, что все финалисты NetOI-2008 умеют решать такую задачу:
Задача о Ханойских башнях
Имеются три стержня A, B, C и N колец разных диаметров, которые можно надевать на стержни. Сначала все кольца находятся на одном стержне (А) в порядке убывания их диаметров (диаметр верхнего кольца 1, а нижнего - N). Необходимо за минимальное количество ходов переместить всю пирамиду на стержень С, используя в качестве вспомогательного стержень B, соблюдая при этом два правила:
- за один ход можно перенести только одно кольцо;
- любое кольцо можно надевать либо на пустой стержень, либо на стержень с верхним кольцом большего диаметра.
Задача состоит в определении последовательности перемещений колец для переноса их с A на С
- за один ход можно перенести только одно кольцо;
- любое кольцо можно надевать либо на пустой стержень, либо на стержень с верхним кольцом большего диаметра.
Задача состоит в определении последовательности перемещений колец для переноса их с A на С
Но на сей раз после решения задачи конечный стержень становится начальным, вспомогательный - конечным, начальный - вспомогательным и игра продолжается без перерыва. Потом вспомогательный стержень станет начальным, начальный - конечным, конечный - вспомогательным и т.д. От начала игры с N дисками сделано K ходов. Определите, сколько раз перекладывался диск диаметром T.
Технические условия
Программа Newhanoy читает с клавиатуры три натуральных числа N - количество дисков, (1 <= N < 64), T - диаметр нужного диска (1<=T<=N), K - количество ходов (1<= K <263). Программа выводит на экран одно число – искомую величину.
Пример
Ввод: 3 3 10
Вывод: 1
Задача Dinner
Жюри, работая над задачами 4 тура, решило прерваться на обед. В школьной столовой шумно - это 1-Б класс обедает. Учительница, увидев уважаемое жюри за столом, начала успокаивать своих шумных учеников. Естественно, слышит ее только тот первоклассник, к которому она обращается. Успокоив одного, она начинает успокаивать следующего. Интересно, сможет ли жюри хоть минутку поесть в тишине, если всех первоклассников N (1<N<=103), каждого i-того нужно успокаивать ai минут, после чего bi минут он будет есть молча, и если да, в каком порядке нужно их успокаивать (1<= ai , bi <=106 ).
Технические условия
Программа Dinner читает с клавиатуры число N, вторая строка ввода содержит N чисел ai , третья N чисел bi . Программа выводит на экран N чисел – порядок, в котором нужно успокаивать первоклассников. Если это сделать не удастся, выводит -1
Примеры |
1 10 10 20 Вывод 2 1 |
Ввод 2 10 10 10 10 Вывод -1 |
Задача Minodd
Господин Дывак решил поехать к своей сестре. Планируя поездку, он узнал о стоимости проезда на всех автобусных рейсах их района. Но господин таки был чудак, потому что решил, что стоимость проезда к сестре должна составлять нечетное число копеек. С другой стороны, он хочет добраться дешевле всего, то есть найти самый дешевый среди тех маршрутов, в которых суммарная стоимость поездки является нечетной. Пересадки Дывака не пугают. Отдельные части маршрута могут стоить четное число копеек; нечетной должна быть суммарная стоимость всех использованных маршрутов.Рейсы выполняются между N населенными пунктами, среди которых село господина Дывака обозначено как №1, сестры — как №2. Для каждой пары пунктов или вообще не существует прямого сообщения, или стоимость проезда известна и одинакова в обоих направлениях. Из любого пункта гарантированно можно добраться до любого, но не исключено, что все возможные способы будут стоить четное число копеек.
Технические условия
Программа Minodd в первой строке читает с клавиатуры числа N и M — количество населенных пунктов и количество рейсов. Дальше считывает M строк по три натуральных числа i, j и cij — номера пунктов, которые соединяет рейс, и стоимость проезда. Среди этих M строк ни разу не повторяется одна и та же пара пунктов (в т.ч., когда те же два пункта переставлены местами). Никакой рейс не соединяет пункт сам с собой. 4≤N,M ≤ 500, 1≤c≤1000. Программа выводит на экран два числа через пробел - минимальную возможную суммарную стоимость проезда среди всех «нечетных» и минимальную возможную стоимость проезда среди всех возможных («четных», или «нечетных») маршрутов. Если не существует ни одного способа добраться за нечетную стоимость, первое число -1.
Пример
Ввод
4 5
1 2 202
1 3 202
1 4 202
2 4 202
3 4 101
Вывод 505 202
Задача Triangles
В Стране Правильных Треугольников (СПТ) города расположены в узлах бесконечной сети дорог, показанной на рисунке. Длина дороги между ближайшими городами составляет 1 УК (условный километр), то есть каждый город соединен дорогами с 6 другими городами. Города задаются координатами, столица страны – начало координат. Король СПТ планирует посетить один из городов. Естественно, путь Его Величества всегда начинается в столице. Однако Его Величеству хочется проезжать только по дорогам и только так, чтобы каждый следующий город находился строго ближе к цели ( в геометрическом смысле, т.е. по прямой), чем ранее посещенный, включая столицу. Чтобы подсчитать количество различных маршрутов короля, советники Его Величества обратились к Вам. Помогите им.
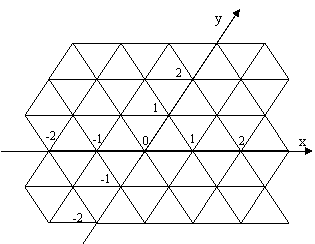
Технические условия.
Программа Triangles читает с клавиатуры через пробел координаты города x,y – целые числа, не превосходящие 200 по абсолютной величине. Программа выводит на экран искомое количество маршрутов по модулю 1000000007
.Пример
Ввод 2 -2
Вывод 5
Задача Maxsum
Жюри думает, что вам приходилось решать такую задачу:
«Имеется прямоугольная таблица размером M строк на N столбцов. В каждой клеточке записано целое число. По ней нужно пройти сверху вниз, начав путь в какой-либо клеточке верхней строки, дальше каждый раз переходя в одну из «нижне-соседних» клеточек (другими словами, из клеточки с номером (i, j) можно перейти или к (i+1, j–1), или к (i+1, j), или к (i+1, j+1); в случае j=N возможные лишь 1-й и 2-й из трех перечисленных вариантов, в случае j=1 — лишь 2-й и 3-й) и закончить маршрут в какой-либо клеточке нижней строки.
Напишите программу, которая будет находить максимально возможную сумму значений пройденных клеточек среди всех допустимых путей»
Решите данную задачу при дополнительном ограничении: допускаются лишь пути, которые проходят (хотя бы по одному разу) через все столбики
. «Имеется прямоугольная таблица размером M строк на N столбцов. В каждой клеточке записано целое число. По ней нужно пройти сверху вниз, начав путь в какой-либо клеточке верхней строки, дальше каждый раз переходя в одну из «нижне-соседних» клеточек (другими словами, из клеточки с номером (i, j) можно перейти или к (i+1, j–1), или к (i+1, j), или к (i+1, j+1); в случае j=N возможные лишь 1-й и 2-й из трех перечисленных вариантов, в случае j=1 — лишь 2-й и 3-й) и закончить маршрут в какой-либо клеточке нижней строки.
Напишите программу, которая будет находить максимально возможную сумму значений пройденных клеточек среди всех допустимых путей»
Решите данную задачу при дополнительном ограничении: допускаются лишь пути, которые проходят (хотя бы по одному разу) через все столбики
Технические условия
Программа Maxsum читает с клавиатуры M и N количество строк и количество столбцов (2≤M≤200, 2≤N≤40, M>=N), далее в каждой из последующих M строк считывается ровно по N разделенных пробелами целых чисел (каждое не превышает по модулю 1 000 000) — значения клеточек таблицы. Программа выводит на экран единственное число – искомую величину.
Пример
Задание подготовили Г.Кравец, Г.Непомнящий, И.Порубльов, Ю.Пасихов
Пример
|
Ввод |
Вывод |
| 4 3 1 15 2 9 7 5 9 2 4 6 9 –1 |
28 |
Задание подготовили Г.Кравец, Г.Непомнящий, И.Порубльов, Ю.Пасихов


