| 29 апреля - 4 мая 2002 года |
|
Міністерство освіти і науки України IX міжрегіональна олімпіада з математики, фізики та інформатики"Турнір чемпіонів"Завдання з математики
1. Послідовність цілих чисел a1 , a2 , a3 , … така, що a1=1,a2=2 і для кожного натурального n>=1
Чи існує таке натуральне число m , що am=2000 ? 2. Точка P знаходиться зовні кола w з центром O . Прямі l1 та l2 проходять через точку P , причому l1 дотикається кола w в точці A , а l2 перетинає w в точках B і C . Дотичні до кола w в точках B і C перетинаються в точці Q . Нехай K - точка перетину прямих BC і AQ . Доведіть, що 3. Знайти всі функції 1) | f(x)| >=1 для всіх дійсних X ; 4. Нехай 5. На площині проводять три набори паралельних прямих, по десять прямих в кожному наборі. На яку найбільшу кількість трикутників вони розріжуть дану площину? На виконання роботи відведено 4 год. Використання калькуляторів та записничків забороняється. |




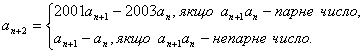
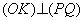 .
.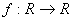 такі, що
такі, що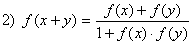 для всіх дійсних X та Y .
для всіх дійсних X та Y .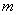 і
і 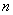 - натуральні числа, які задовольняють нерівність
- натуральні числа, які задовольняють нерівність 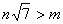 . Доведіть, що тоді виконується й така нерівність
. Доведіть, що тоді виконується й така нерівність 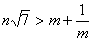 .
.