|
|
Математика
1.Нехай 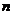 – таке натуральне число, що – таке натуральне число, що 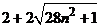 – ціле число. Доведіть, що і – ціле число. Доведіть, що і
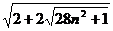 також ціле число. також ціле число.
2. Дано трикутник 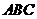 . Пряма, яка проходить через вершину . Пряма, яка проходить через вершину 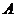 , симетрична медіані , симетрична медіані 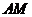 відносно прямої, що містить бісектрису кута відносно прямої, що містить бісектрису кута 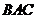 , перетинає коло, описане навколо трикутника , перетинає коло, описане навколо трикутника 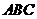 , в точках , в точках 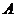 і і 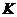 . Нехай . Нехай 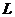 – середина відрізка – середина відрізка 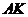 . Доведіть, що . Доведіть, що 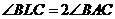 . .
 3. Перша абетка, яку вивчають учні початківці Вінницької фізико-математичної гімназії №17, містить лише три літери 3. Перша абетка, яку вивчають учні початківці Вінницької фізико-математичної гімназії №17, містить лише три літери 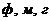 . Обчисліть кількість слів, кожне з яких можна записати . Обчисліть кількість слів, кожне з яких можна записати 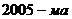 літерами цієї абетки і кожне з яких містить парну кількість літер літерами цієї абетки і кожне з яких містить парну кількість літер 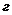 . .
4. Доведіть, що для будь-яких дійсних додатних чисел 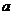 , , 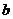 , , 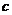 виконується нерівність виконується нерівність
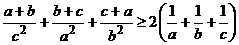 . .
Математика
1. Пусть n – такое натуральное число, что 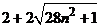 - целое число. Докажите, что и - целое число. Докажите, что и 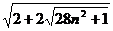 тоже целое число. тоже целое число.
2. Дан треугольник АВС. Прямая, проходящая через вершину А , симметрична медиане АМ относительно прямой , содержащей биссектрису угла ВАС, пересекает окружность, описанную около треугольника АВС, в точках А и К. Пусть L –середина отрезка АК. Докажите, что 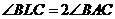 . .
3. Первый алфавит, который изучают ученики–первоклассники Винницкой физико-математической гимназии №17, содержит всего три буквы ф, м, г. Вычислить количество слов, каждое из которых можно записать 2005-ю буквами этого алфавита и каждое из них содержит четное количество букв г.
4. Докажите, что для любых вещественных (действительных) положительных чисел a, b, c выполняется неравенство:
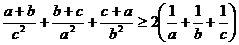 . .
|