XІІI Всеукраїнська комплексна олімпіада з математики, фізики
та інформатики

"Турнір чемпіонів"
2006 р.
Задания по информатике
Задача Двуствольная пушка (DGUN)
Цель компьютерной игры WALLCRSH – разбить все плиты, укреплённые на стенах оборонной башни противника. Башня имеет вид правильного многоугольника с N вершинами (т.е. каждая стена башни является стороной многоугольника). Для разрушения плит игрок использует специальную двуствольную пушку, каждый выстрел которой разрушает (в зависимости от желания игрока) либо две плиты на одной и той же стене башни, либо по одной плите на двух соседних стенах. Стрельба по стенам, на которых не осталось плит, не запрещается, но это считается расточительством.
Найдите, за какое минимальное количество выстрелов можно разрушить все плиты.
Формат ввода/вывода:
Напишите программу DGUN, которая читает входные данные из файла DGUN.DAT и записывает ответ в файл DGUN.SOL. В первой строке файла DGUN.DAT находится количество стен, во второй – разделённые пробелами количества плит на каждой стене 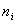 .
.
Файл DGUN.SOL должен содержать единственное число – минимальное количество выстрелов.
Ограничения: 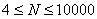 ,
, 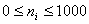
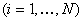 .
.
Пример:
|
DGUN.DAT 6 3 2 2 1 1 3 |
DGUN.SOL 6
|
 Задача Эмблема (LOGO)
Задача Эмблема (LOGO)
Фирма K&K заказала у вас новую эмблему для своей продукции. Они желают, чтобы эмблема выглядела, как два пересекающихся квадрата. Сами квадраты должны быть черными, а их пересечение – белым (Один из вариантов эмблемы вы можете видеть на рисунке).
Вам надо найти площадь черных частей эмблемы, чтобы определить, сколько краски потребуется для рисования эмблемы.
Замечание: квадраты на эмблеме могут пересекаться произвольным образом, в частности они могут быть вложены один в другой или касаться друг друга.
Формат ввода/вывода:
Напишите программу LOGO, которая читает координаты двух квадратов из файла LOGO.DAT и записывает ответ в файл LOGO.SOL.
В двух строках файла LOGO.DAT записаны координаты квадратов. В каждой строке записано по четыре вещественных числа: 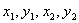 – координаты двух противоположных вершин квадрата.
– координаты двух противоположных вершин квадрата.
Файл LOGO.SOL должен содержать единственное число – площадь фигуры, которую нужно закрасить, вычисленная с точностью до 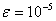 (т.е. ваш ответ не должен отличаться от ответа жюри больше чем на
(т.е. ваш ответ не должен отличаться от ответа жюри больше чем на 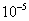 ).
).
Ограничения: 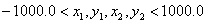 .
.
Пример:
|
LOGO.DAT: 0.0 1.0 3.0 4.0 2.0 3.0 4.0 5.0 |
LOGO.SOL: 11.0 |
Задача Часы на сканере (SCAN)
Секундная стрелка часов перемещается скачкообразно, т.е. на протяжении секунды неподвижна, а потом мгновенно поворачивается на 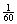 полного оборота. Стрелка представляет собой тонкий отрезок длины d мм, исходящий из центра часов.
полного оборота. Стрелка представляет собой тонкий отрезок длины d мм, исходящий из центра часов.
Часы положили на сканер ориентировав обычным образом (отметка 12 сверху) и подобрали параметры сканирования так, что:
1. Сканирование запускается сразу же после того, как секундная стрелка совершила очередной прыжок и начала показывать s секунд.
2. Область сканирования выбрана размером 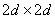 мм2 так, что она в точности вмещает окружность, которую описывает секундная стрелка.
мм2 так, что она в точности вмещает окружность, которую описывает секундная стрелка.
3. Сканер за 1 с успевает получить прямоугольное изображение высотой ровно k мм.
4. Разрешающая способность сканирования достаточно высока, чтобы можно было пренебречь дискретностью изображений внутри каждой k-миллиметровой полоски и считать расстояния по обычным геометрическим формулам.
Найдите суммарную длину изображений секундной стрелки в полученной картинке (изображения других элементов часов не вносят путаницы, т.к. секундная стрелка резко отличается от них по цвету).
Формат ввода/вывода:
Напишите программу SCAN, которая читает из файла SCAN.DAT три целых числа: k (ширину области, сканируемой за 1 с), d (длину стрелки) и s (момент времени), и выводит в файл SCAN.SOL действительное число l — суммарную длину изображений секундной стрелки, с точностью 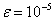 (это означает, что ваш ответ не должен отличаться от ответа жюри больше чем на
(это означает, что ваш ответ не должен отличаться от ответа жюри больше чем на 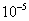 ).
).
Ограничения: 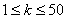 ,
, 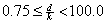 ,
, 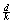 не является целым числом,
не является целым числом, 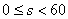 ,
, 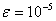 .
.
Пример:
|
SCAN.DAT: 36 90 10 |
SCAN.SOL: 103.994544 |
Задача На дне (BOTTOM)
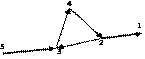 На дне некоторого озера находятся N домиков, в каждом из которых живет по одной черепахе. В гости к ним собирается дружелюбный Краб, который хотел бы поселиться у такой черепахи, живя у которой он бы мог посетить максимальное количество других. Для перемещения между домиками существуют трассы с односторонним движением, которые соединяют два домика, по которым краб может перемещаться нормально и задом наперед. По трассе с движением из A в B краб может перемещаться из A в B, если он перемещается нормально и из B в A, если он перемещается задом наперед.
На дне некоторого озера находятся N домиков, в каждом из которых живет по одной черепахе. В гости к ним собирается дружелюбный Краб, который хотел бы поселиться у такой черепахи, живя у которой он бы мог посетить максимальное количество других. Для перемещения между домиками существуют трассы с односторонним движением, которые соединяют два домика, по которым краб может перемещаться нормально и задом наперед. По трассе с движением из A в B краб может перемещаться из A в B, если он перемещается нормально и из B в A, если он перемещается задом наперед.
Из домика, где поселится Краб, он начинает движение задом наперед. Однако среди всех подводных трасс есть такие, после движения по которым Краб всегда меняет способ своего движения на противоположный. В никаком другом месте кроме этих специальных трасс он не может менять свой способ перемещения.
Посетить другую черепаху Краб может только в том случае, если выходя из домика где он поселился, он может, согласно своим правилам движения, дойти до нужной черепахи и после этого вернуться к той, которая его приютила, причем вернуться так, чтобы по окончанию путешествия направление Краба было опять задом наперед.
Помогите Крабу определить, к какой из черепах ему лучше поселиться, чтобы посетить максимальное количество других подводных обитательниц. А для этого, поскольку Краб недоверчив, подсчитайте для каждого из подводных жилищ количество черепах, которых может посетить Краб, проживая в данном. Причем, очевидно, что черепаху, у которой он живет, посещать не нужно.
Формат ввода/вывода:
Напишите программу BOTTOM, которая читает входные данные из файла BOTTOM.DAT и записывает ответ в файл BOTTOM.SOL.
В первой строке файла BOTTOM.DAT находятся два целых числа 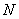 и
и 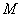 – количество домиков и количество трасс соответственно. В следующих
– количество домиков и количество трасс соответственно. В следующих 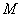 строках находятся описания трасс, по одному в каждой строке. Описание трасс состоит из трёх чисел
строках находятся описания трасс, по одному в каждой строке. Описание трасс состоит из трёх чисел 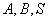 , где
, где 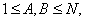 а
а 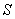 равно
равно 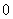 или
или 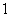 . Число
. Число 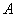 a это номер дома, в котором трасса начинается,
a это номер дома, в котором трасса начинается, 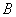 – это номер дома, где заканчивается трасса. Если
– это номер дома, где заканчивается трасса. Если 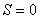 , то трасса обычная, а если
, то трасса обычная, а если 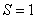 , то трасса специального типа.
, то трасса специального типа.
Файл BOTTOM.SOL должен содержать ровно 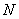 строк, в
строк, в 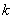 -ой строке должно быть число друзей которых он сможет посетить живя в доме номер
-ой строке должно быть число друзей которых он сможет посетить живя в доме номер 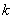 .
.
Ограничения: 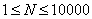 ,
, 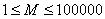 .
.
Пример:
|
BOTTOM.DAT 5 5 2 1 1 2 3 0 3 4 0 4 2 0 5 3 1 |
BOTTOM.SOL 3 3 3 3 0
|
Живя в доме 1, Краб может посетить приятелей в домах 2, 3, 4. Живя в доме 2, Краб может посетить приятелей в домах 3, 4, 5. Живя в доме 3, Краб может посетить приятелей в домах 2, 4, 5. Живя в доме 4, Краб может посетить приятелей в домах 2, 3, 5. Живя в доме 5, Краб не может посетить никого.
Указания к решению задач по информатике
Задача Двуствольная пушка (DGUN)
Рассмотрим, что будет, если сбивать плитки по порядку, начиная с 1-ой стены. Если n1 чётно, то на 1-ую стену надо потратить 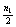 выстрелов, если нечётно – то
выстрелов, если нечётно – то 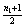 , но при этом удаётся сразу сбить ещё и 1-ую плитку со 2-ой стены. Так приходим к гипотезе, что искомое количество выстрелов всегда равно
, но при этом удаётся сразу сбить ещё и 1-ую плитку со 2-ой стены. Так приходим к гипотезе, что искомое количество выстрелов всегда равно 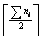 (где ∑ означает сумму,
(где ∑ означает сумму, 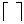 – округление вверх, например
– округление вверх, например 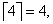
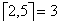 ).
).
Однако это ещё не всё. Поскольку по условию допускается, чтобы некоторые стены не были покрыты плитками (ni=0) «лишний» заряд из последней пары не всегда можно «перенести» на следующую стену. Поэтому упомянутая формула должна применяться отдельно для каждого «кусочка» от ноля до ноля. С другой стороны, поскольку многоугольник является замкнутой фигурой, первый и последний кусочки (если их вообще было больше одного) надо посчитать вместе: сначала сложить количества, а потом уже поделить на 2 и округлить вверх.
Задача Эмблема (LOGO)
Чтобы узнать площадь закрашенной части, достаточно посчитать площади каждого квадрата отдельно, сложить, и отнять из результата удвоенную площадь пересечения (кусочка, принадлежащего обоим квадратам сразу). Таким образом, основная сложность задачи – поиск пересечения квадратов. Например, для этого можно найти точки пересечения квадратов и те вершины, которые лежат внутри или на границе другого квадрата. Если вокруг этих точек описать выпуклую оболочку, то полученная фигура и окажется пересечением квадратов.
Задача Часы на сканере (SCAN)
В данной задаче не надо придумывать супералгоритм, достаточно аккуратно промоделировать процесс. Т.е., для каждой секунды, на протяжении которых будет продолжаться сканирование, выделить видимый прямоугольничек, найти его пересечение с текущим расположением секундной стрелки и посчитать его (пересечения) длину.
Возможные сложности с этой задачей состоят в том, чтобы: правильно считать координаты конца стрелки в зависимости от количества секунд; не забыть, что концы пересечения могут определяться и краями текущего многоугольника, и краями самой стрелки; не забыть, что при количестве секунд от 46 до 14 конец стрелки выше начала, от 16 до 44 – ниже, а при 15 или 45 стрелка вообще горизонтальна.
Задача На дне (BOTTOM)
Для решения задачи удобно построить специальный граф из 2N вершин и 2M рёбер. Его можно представить себе как два слоя: один соответствует «нормальному» направлению передвижения Краба, другой – направлению «задом наперёд». В слое «нормальных» передвижений направления всех дуг соответствуют направлениям движения (не специальных) трасс, во втором слое все дуги направлены противоположно. Специальные трассы задают перемещения между слоями.
Краб может посетить тех и только тех черепах, чьи домики соответствуют вершинам построенного графа, находящимся в той же компоненте сильной связности, что и вершина, соответствующая стартовому домику. Точнее говоря, для стартового домика надо обязательно брать вершину из слоя перемещений «задом наперёд», а для достижимости остальных домиков достаточно, чтобы в компоненту сильной связности вошла хотя бы одна из двух соответствующих ей вершин.
Компонента сильной связности – это множество тех вершин орграфа (+ рёбер, их связующих), для которых, во-первых, существуют пути из каждой вершины в каждую, и, во-вторых, такой набор нельзя расширить, чтобы не нарушилось первое свойство. Поиск всех компонент сильной связности – это стандартный алгоритм, описанный во многих книгах по теории графов (см. напр. Кормен и др. Алгоритмы: построение и анализ).


