XІII Всеукраїнська комплексна олімпіада з математики, фізики
та інформатики
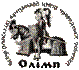
"Турнір чемпіонів"
2006 р.
Фізика
1. Космічний корабель масою М з імпульсним двигуном рухається навколо Землі по еліптичній орбіті з осями: 2a – велика 2b – мала. Як перевести його рух з еліптичної орбіти до колової в той момент коли корабель знаходився на відстані a від центру Землі. Чи можлива інша колова орбіта, але з дещо більшою затратою енергії? Примітка: двигун включається лише раз. Визначити модуль зміни швидкості та напрямок такої зміни.
2 . Заряженный шарик привязан к одному из концов невесомой нерастяжимой нити. Другой конец нити закреплен. Шарик движется по окружности в плоскости, перпендикулярной магнитному полю (нить тоже находится в этой плоскости). Частота вращения такова, что сила натяжения нити равна нулю. Во сколько раз изменится частота вращения шарика, если магнитное поле медленно выключать? Тяготение отсутствует.
3. Вода без примесей нагревается до температуры 101ºС при внешнем давлении P = 1 атм. Оценить минимальный размер песчинки, которая при попадании в воду вызовет вскипание воды. Коэффициент поверхностного натяжения воды 58,8·10–3 Н/м, удельная теплота парообразования 2,26·106 Дж/кг, удельный объем водяного пара 1,7 м3/кг при 100ºС.
3. К большему металлическому листу толщиной a приварены на расстоянии b друг от друга два цилиндрических проводника радиусом r0. Найти сопротивление R между проводниками, если a<<r0<<b. Считать, что удельная проводимость λ1 проводников значительно больше проводимости λ материала листа.

Задание для 8-9 классов
1) Имеются два теплоизолированных сосуда. В первом из них находится 5 л воды при температуре 60ºС, во втором – один литр воды при температуре 20ºС. Вначале часть воды перелили из первого сосуда во второй. Затем, когда во втором сосуде установилось тепловое равновесие, из него в первый сосуд отлили столько воды, чтобы ее объемы в сосудах стали равны первоначальным. После этих операций температура воды в первом сосуде стала равной 59ºС. Сколько воды переливали из первого сосуда во второй и обратно?
Решение:
|
t1 = 60ºС t2 = 20ºС t4 = 59ºС V1 = 5 л V2 = 1 л ΔV – ? |
В результате переливаний в замкнутой системе общая энергия системы сохранится. Так как сохранилось и количество воды в обоих сосудах, то в общем от первого сосуда ко второму было передано некоторое количество теплоты ΔQ: ΔQ = c·ρ·V1·(t1 – t4) = c·ρ·V2·(t3 – t2), где t3 – температура во втором сосуде после первого переливания: |
Записав уравнение теплового баланса для одного из процессов, например, первого переливания:
c·ρ·ΔV·(t1 – t3) = c·ρ·V2·(t3 – t2),
получим:
Подставив t3, находим окончательное выражение:
Ответ:
2) Прямоугольный сосуд с водой стоит на двух опорах, разнесенных на расстояние L друг от друга. Над сосудом на перекладине подвешен на нити кусок свинца массой M на расстоянии l от центра сосуда см. рис. Силы реакции опор при этом равны N1 и N2. Нить удлиняют так, что свинец погружается в воду. Какими станут после этого силы реакции опор? Плотность свинца в n раз больше плотности воды.
Решение:
|
N1 N2 l; L; M;
ΔV – ? |
|
В первоначальном состоянии силы реакции опор можно определить из системы уравнений:
– равенство нулю суммы сил: (m + M)·g = N1 + N2 (1)
– правило моментов относительно точки О: (2)
После опускания свинца в воду силы реакции опор (T1 , T2) изменятся в соответствии с уравнением: (3)
Так как внешние по отношению к системе сосуд-вода-свинец не изменились, то не изменилась и сумма сил реакции опоры. Перепишем систему уравнений (1)-(3) в виде:
T1 + T2 = N1 + N2
Откуда ответ:
3) На рисунке приведены вольтамперные характеристики двух нелинейных резисторов R1 и R2. Какими будут мощности, которые выделяются на каждом из нелинейных резисторов, если соединение резисторов подключить последовательно к источнику с напряжением 10 В и к линейному резистору сопротивлением 2 Ом? В соединении нелинейные резисторы включены:
а) параллельно; б) последовательно.
Решение:
|
R1 R2 U = 10 В P1, P2 – ? |
|
a) Параллельное соединение:
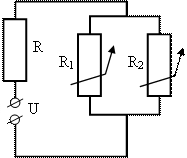
I = I1 + I2; U = U1 = U2;
Графическое сложение по значениям силы тока дает кривую I, которая в сумме с падением напряжения на обычном резисторе (прямая) должна дать 10 В.
U1 = U2 = U – I·R = 10 – 2·I ;
Точка пересечения с линейной зависимостью дает нам возможность определить, что
U1 = U2 = 8,2 В.
Тогда (по графику) I1 = 0,52 А; I1 = 0,38 А.
P1 = I1·U1 = 8,2·0,52 A = 4,3 Вт
P2 = I2·U2 = 8,2·0,38 A = 3,1 Вт
b) Последовательное соединение:
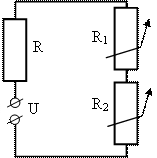
I = I1 = I2; U = U1 + U2;
Графическое сложение по значениям напряжения дает кривую II. Аналогично предыдущему случаю, получаем (см. график):
I = I1 = I2 = 0,27 А;
U1 = 5,2 В; U2 = 4,3 В;
P1 = I1·U1 = 0,27·5,2 В = 1,4 В;
P2 = I2·U2 = 0,27·4,3 В = 1,2 В.
Мальчик переплывает через реку под углом 30º к берегу, один раз за две минуты, другой раз, по той же траектории, в ту же сторону, за 4 минуты. Как соотносятся скорость пловца относительно воды и скорость течения реки? Скорость пловца относительно воды оба раза была одинаковая.
Решение:
|
t1 = 2 мин t2 = 4 мин α = 30º
– ?
|
|
Как видно из рисунка, пловец двигался в первый раз с в два раза большей скоростью так как меньше сил затрачивал на борьбу с течением реки. Также очевидно, что такое движение возможно только при скорости течения реки большей, чем скорость пловца. Рассмотрим получившийся треугольник:
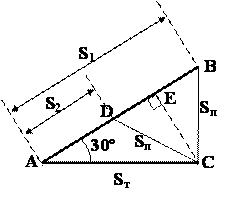
где S1 – путь, пройденный пловцом в первый, S2 – во второй раз, Sт – расстояние, на которое его сносит река. Соотношение времен движения определяет DC как медиану ΔABC. Тогда
.
Так как , то ÐDCE = 30º. Тогда
.
Ответ:
4) Две плиты приближаются друг к другу с постоянной скоростью V. Между плитами перпендикулярно их плоскости движется шарик со скоростью v много большей, чем V. Первоначально расстояние между пластинами L. Какую скорость будет иметь шарик, когда расстояние между пластинами станет равным L1?
Решение:
|
V << v v, L L1 v1 |
|
При абсолютно упругом ударе шарика о пластину его скорость увеличивается на 2V. К тому моменту, когда расстояние между пластинами будет L1, и произойдет большое число ударов – n, скорость шарика будет:
v1 = v + 2·n·V. (1)
За это время расстояние между пластинами будет:
L1 = L – 2·V·t . (2)
В силу того, что пластины движутся медленно, по сравнению с шариком, расстояние между ними уменьшается медленно, а скорость шарика медленно возрастает можно считать, что среднее расстояние будет пройдено со средней скоростью . Тогда
. (3)
Система уравнений (1)-(3), при исключении n и t дает:
v1 L1 = v L .
Второй вариант решения с использованием производных:
В силу малости скорости V относительно v можно считать изменение n непрерывным. Тогда за время dt произошло dn столкновений. Приращение скорости за это время
dv = 2·V dn
За это время расстояние между пластинами изменится до x в соответствии с:
За все время движения t расстояние между пластинами станет: L1 = x = L – 2·V·t .
Тогда
Откуда после интегрирования имеем:
Ответ: Когда расстояние станет L1 скорость будет .