Задання фінального (Real Time) туру NetOI-2021
13 лютого 2022 р.
Попередній коментар. Ми свідомі того, що в умовах карантиннних обмежень (в різних регіонах - різних) оргкомітет не в змозі забезпечити належні умови контролю академічної та наукової доброчесності під час туру. Доступні методи контролю малоефективні, і, при наявності бажання, легко обходяться. Тому журі олімпіади щиро вірить в порядність та доброчесність фіналістів. Отримана нечесним способом перемога нікому не зможе принести щастя - життя все рівно розставить все по своїм місцям - якщо не зараз, то раніше чи пізніше - але обов'язково!
Задача Trolley2022
У Василя Голопупенка дві особливості. По-перше, він добре знає розклад свого улюбленого тролейбуса №7, який ходить під вікнами його будинку (та до того ж ніколи не спізнюється). По-друге, він абсолютно не вміє дізнаватися час за годинником, лише за положенням сонця та зірок (та й то лише приблизно). Щоразу, коли Василь прокидається, він біжить до вікна - оцінити поточний час і дочекатись наступного тролейбуса. Вася згадав останні M разів, коли він прокидався (щоразу приблизно між Li та Ri ), і йому стало цікаво порівняти середній теоретичний час очікування і реальний. Середнім теоретичним часом очікування Вася вважає час, який у середньому він би прочекав тролейбус, якби рівноймовірно прокинувся у довільний цілочисельний момент часу між Li та Ri . Таким чином, нехай f(t) - теоретичний час очікування наступного тролейбуса з моменту t, тоді середній теоретичний час між Li та Ri - це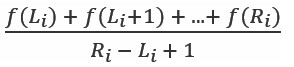 
Вашою задачею є віднайти чисельник цього дробу, тобто f(Li) +f(Li +1)+ ...+f(Ri) (бо знаменник Вася і так знає) для кожної пари Li та Ri.
Технічні умови Програма Trolley2022 зчитує з пристрою стандартного введення у першому рядку 3 числа - N, M, K (1 ≤ N, M ≤ 105, 1≤ K ≤ 109). N - кількість часових відміток у розкладі тролейбуса, M - кількість запитів, для яких Василь хоче дізнатися результат, та K - кількість хвилин у добі на планеті Василя.
Далі слідують рівно N чисел Ti (1 ≤ Ti ≤ K) (у відсортованому порядку) - усі моменти у добі, коли тролейбус проїжджає поруч з будинком Василя..
Далі слідує рівно M пар чисел Li Ri (1 ≤ Li ≤ Ri ≤ K) - запити Василя (в одному рядку).
Програма має вивести рівно M цілих чисел в одному рядку - відповіді на запити.
ПРИКЛАД
|
Введення |
Виведення |
Коментар |
|
3 3 8 2 4 7 2 4 7 8 1 8 |
1 2 7 |
У першому випадку Васі потрібно чекати або 0 (у варіанті часу прокидання 2), або 1 (у випадку 3), або 0 (у випадку 4). У сумі 1. У другому випадку Вася прокидається або о 7-ій хвилині і одразу бачить тролейбус, або о 8-ій і йому доведеться чекати наступної доби (перший тролейбус буде о другій хвилині, тобто рівно за 2 хвилини). У третьому випадку маємо сумарний теоретичний час очікування 1 + 0 + 1 + 0 + 2 + 1 + 0 + 2 = 7 |
Задача Diagno2022. Ви працюєте в лабораторії, що досліджує дію речовин на живі організми. Вам достеменно відомо, що серед N речовин рівно одна смертельно небезпечна. Є K тваринок. Якщо такій тваринці ввести небезпечну речовину, то тваринка загине рівно через годину. Речовини між собою не взаємодіють. Ви можете одній тваринці вводити одночасно кілька речовин. За який мінімальний час у найгіршому випадку Ви зможете визначити небезпечну речовину?
Технічні умови. Програма Diagno2022 читає з пристрою стандартного введення числа N, K 1≤N,K≤1018) і виводить на пристрій стандартного виведення шуканий час.
Приклади
Введення 3 2
Виведення 1
Введення 5 1
Виведення 4
Задача Boxes2022. Напишiть програму, яка знаходитиме перелiк прямокутних паралелепiпедiв, що мають об’єм 𝑉 та площу поверхнi 𝑆. Враховувати лише паралелепiпеди, в яких всi три розмiри виражаються натуральними числами.
Технічні умови . Програма Boxes2022 читає з пристрою стандартного введення два натуральнi числа 𝑉 (1≤V≤1018), 𝑆 (1≤S≤1017) , розділені пропуском. Програма виводить на пристрій стандартного виведення в одному рядку через пропуски групи по 3 числа - цiлочисельнi розмiри 𝑎 𝑏 𝑐 чергового паралелепiпеда. Цi трiйки обов’язково виводити у порядку зростання першого розмiру 𝑎, при рiвних 𝑎 — у порядку зростання др´угого розмiру 𝑏 (а рiзних вiдповiдей, в яких рiвнi i 𝑎, i 𝑏, не буває). У випадку, якщо жодного паралелепiпеда з потрiбними 𝑉 , 𝑆 не iснує, виводьте єдиний рядок 0 0 0.
Примiтка. Якщо прямокутний паралелепiпед має розмiри 𝑎 𝑏 𝑐, то його об’єм дорiвнює 𝑎 · 𝑏 · 𝑐, а площа поверхнi 2 · (︀ 𝑎 · 𝑏 + 𝑏 · 𝑐 + 𝑐 · 𝑎 )︀ , бо є двi гранi (наприклад, передня й задня) площi 𝑎 · 𝑏, двi (наприклад, лiва та права) площi 𝑏 · 𝑐 та двi (наприклад, верхня й нижня) площi 𝑐 · 𝑎.
Приклад
Введення 7 7
Виведення 0 0 0
Введення 6 22
Виведення 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
Введення 1 6
Виведення 1 1 1
Введення 1600 1120
Виведення 4 20 20 5 8 40 5 40 8 8 5 40 8 40 5 20 4 20 20 20 4 40 5 8 40 8 5
Задача Horse2022. На шахівниці NxM клітинок живе Кінь Подільський. Кінь Подільський дуже сильний і може стрибати скільки завгодно за стандартними правилами ходу шахового коня. (2x1) за один свій хід. Король-суперник отримав суперсилу "виколювати" клітинки. Кількість усіх виколотих клітинок K. Кінь не може на них ставати. Зате може ставати на всі інші, якщо вони, звісно, досяжні за скінченну кількість ходів звичайного шахового коня (2x1). Кінь Подільський прудкий і гордий, він намагається тримати всі невиколоті клітинки під контролем.
Дано послідовність X[i], Y[i] у якому король-суперник "виколює" клітинки. Спочатку вся шахівниця доступна для відвідування конем. Всі клітинки у послідовності - унікальні, їх координати (X, Y) не повторюються. Після якого найпершого кроку i короля-суперника кінь не зможе тримати всі невиколоті клітинки під контролем? Якщо такого кроку не існує - виведіть -1. (Тримати під контролем - це мати можливість потрапити з будь-якої невиколотої клітинки у будь-яку невиколоту класичними ходами шахового коня по невикоотим клітинкам)
Технічні умови. Програма Horse2022 читає з пристрою стандартного введення натуральні числа N,M,K (3 ≤ N, M ≤ 3000, N*M≤105 , 1≤ K ≤ N*M-1). Далі програма читає K рядків по 2 числа в кожному – координати виколотих клітинок X[i] та Y[i] (1 ≤ X[i] ≤ N,1 ≤ Y[i] ≤ M). Програма виводить на пристрій стандартного виведення шуканий номер.
Приклад
Введення
3 4 6
1 1
1 3
2 2
2 4
3 1
3 3
Виведення
3
Коментар. Поле (3,4) після третього ходу короля недосяжне з інших.
Задача Tickets2022. Правила перевезень пасажирів поїздами дальнього сполучення передбачають, що у квитку вказується конкретне місце. Мати відоме гарантоване місце (і знати про це наперед) досить зручно. Але це правило може спричинювати проблему хибної відсутності місць.
Розглянемо малоймовірний, але теоретично можливий випадок. Нехай поїзд прямує зі станції A до станції C з єдиною зупинкою по станції B, і одна половина місць продані від A до B, інша половина — від B до C. Тоді неможливо купити жодного квитка від A до C. Хоча, якщо здогадатися, можна купити досить багато квитків окремо від A до B й окремо, на інші місця, від B до C, й таким чином доїхати від A до C.
Напишіть програму, яка шукатиме загальну кількість таких пар станцій, між якими вже не можна купити квитка ні на яке конкретне місце, але якщо по дорозі переходити з місця на місце, то доїхати можна.
Технічні умови. Програма Tickets2022 читає з пристрою стандартного введення з першого рядка - кількість місць у поїзді k (3≤k≤1000) через пропуск - кількість станцій у маршруті n (3≤n≤10000) і кількість проданих квитків t (0≤ t ≤min(105, k∙(n–1))). Кожен з подальших t рядків містить по три числа pl, st, fn, які задають квиток: pl — номер місця (нумерація від 1 до k, наскрізна по всьому поїзду, без розбивки по вагонам), а st та fn означають, що квиток діє від станції номер st до станції номер fn (станції пронумеровані уздовж маршруту, від 1 до n). У кожному квитку st < fn, тобто номер станції призначення строго більший номера станції відправлення. Різні квитки на одне й те саме місце можливі лише якщо їхні проміжки дії не накладаються (кожен наступний квиток може починатися або зі станції, на якій закінчився попередній, або пізніше). Програма виводить на пристрій стандартного виведення єдине ціле число — шукану кількість пар станцій.
|
Введення |
Виведення |
|
3 10 6 2 9 10 3 5 9 1 2 10 2 1 4 2 7 8 3 1 2 |
10 |
Примітка. Ці 10 пар — (1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (2, 6), (2, 7), (3, 6), (3, 7), (8, 10). Для решти пар станцій або можна купити квиток з місцем, або доїхати неможливо, навіть перебираючись з місця на місце.
Завдання підготували М. Бевза, Г.Непомнящий, М.Стречень, І. Порубльов, Ю.Пасіхов