ЗАВДАННЯ 3-го туру Всеукраїнської Інтернет-олімпіади NetOI-2021
Розв'язки приймаються до 0 годин 3.02.22
Задача Mount2021. Профіль Кирпатих гір задається ламаною (x1, y1), (x2, y2), …, (xN, yN), для координат вершин якої виконуються нерівності x1 < x2 < … < xN. Ви можете побудувати прямолінійний тунель, що з’єднує дві точки цієї ламаної. Вам необхідно спроектувати дорогу з точки A(x1, y1) в точку B(xN, yN). Ця дорога буде проходити по схилах гір і через тунель. Обидва кінці тунелю знаходяться на гірському профілі. Дорога заходить у тунель з одного кінця та виходить з іншого, більше тунель ніде не виходить на поверхню. Напишіть програму, яка обчислює найменшу можливу довжину дороги з точки А в точку В.
Технічні умови.Програма Mount2021 читає з пристрою стандартного введення з першого рядка натуральне число N (2<=N<=100000), далі з наступних N рядків N пар натуральних чисел, не більших 1000000000 – координати вершин ламаної. Програма виводить на пристрій стандартного виведення єдине дійсне число – мінімальну довжину дороги з максимально можливою для вашого компілятора точністю
Приклади
|
Введення |
Виведення |
Коментар. У першому прикладі тунель не будуємо. У другому прикладі можна з`єднати першу точку з третьою або третю з п’ятою. |
|
3 1 6 4 2 7 6 |
10.0000000
|
|
|
Введення |
Виведення |
|
|
5 1 2 4 6 7 2 10 6 13 2 |
16.0000000
|
Задача Galaxy2021. Давним-давно в далекій-далекій галактиці було N планет. Міжпланетний шлях, з’єднував дві різні планети. Було N − 1 міжпланетних шляхів, що з'єднували всі планети (прямо чи опосередковано). Іншими словами, мережа планет і шляхів утворили дерево. Крім того, кожен шлях мав свою цікавість – ціле невід’ємне число. Пара планет A, B є нудною, якщо виконується наступне:
• А і В — різні планети
• подорож між планетами А і В можлива за допомогою одного або кількох міжпланетних шляхів
• двійкове XOR цікавості всіх шляхів у цій подорожі дорівнює 0.
На жаль, часи змінилися, і злий імператор править галактикою. Він вирішив використати Силу, щоб знищити всі міжпланетні шляхи в певному порядку. Визначте кількість нудних пар планет до того, як імператор почав руйнування і після кожного руйнування.
Технічні умови. Програма Galaxy2021 читає з пристрою стандартного введення з першого рядка ціле число N (1≤N≤100000). Далі програма читає N − 1 рядків, кожний з яких містить три цілі числа Ai, Bі, Zi (1≤Ai,Bi≤N, 0≤Zi≤1000000000), які означають, що планети Ai і Bi безпосередньо пов'язані шляхом цікавості Zi. З наступного рядка програма читає перестановку перших N − 1 цілих чисел, які позначають порядок, у якому імператор руйнує шляхи. Якщо i-й елементом перестановки є j, тоді імператор знищив шлях між планетами Aj і Bj в i-й крок. Програма виводить на пристрій стандартного виведення в одному рядку через пропуск N чисел. K-е число - кількість нудних пар A, B з завдання після того, як імператор знищив рівно K − 1 шляхів.
Приклади
|
Введення 2 1 2 0 1 |
Виведення 1 0
|
Пояснення першого прикладу: До руйнування пара (1, 2) нудна. Після руйнування, шлях між ними більше не існує.
Пояснення другого прикладу: до руйнування пара планет (1, 3) нудна. Подорож між 1 і 3 більше неможлива після першого і після другого руйнування, тому не існує жодної нудної пари.
Пояснення третього прикладу: Зверніть увагу, що в цьому прикладі кожна пара планет має можливий шлях між ними, тому що всі шляхи мають цікавість 0.
|
|
Введення 3 1 2 4 2 3 4 1 2 |
Виведення 1 0 0
|
|
|
Введення 4 1 2 0 2 3 0 2 4 0 3 1 2 |
Виведення 6 3 1 0
|
Задача Stroll. На паличці довжиною L метрів сидить N блямблянчиків. Кожен блямблянчик рухається вздовж палиці з постійною швидкістю 1 м/с в одному з двох можливих напрямків (ліворуч або праворуч) і забарвлений в один із можливих K кольорів.
Відомо, що блямблянчики живуть по законам, які вказують: прогулянку вздовж палиці потрібно продовжувати доти, поки не буде досягнуто кінця палиці (що означає злізти з неї), а коли відбувається зіткнення з іншим блямблянчиком, потрібно розвернутися на 180 градусів і продовжити рух в протилежному напрямку. Крім того, після того, як блямблянчик кольору a, що рухається вліво, стикається з блямблянчиком кольору b, що рухається праворуч, то той, який рухався ліворуч перед зіткненням, приймає колір того, який рухався вправо перед зіткненням (тобто, колір b), тоді як блямблянчик, що рухався перед зіткненням вправо, набуває нового кольору (a + b) mod K. Вам дано початкові положення, кольори та напрямки руху всіх блямблянчиків. Визначте для кожного кольору загальну довжину шляхів блямблянчиків цього кольору, перш ніж усі вони зійдуть з палиці.
Технічні умови. Програма Stroll читає з пристрою стандартного введення з першого рядка цілі числа: кількість блямблянчиків N, кількість кольорів K і довжину палиці L (1 ≤ N ≤ 100000, 1 ≤ K ≤ 40, 1 ≤ L≤1000000). Далі програма читає з наступних N рядків ціле число di (0 ≤ dі ≤ L), що позначає відстань між і-м блямблянчиком і лівим кінцем палиці, потім ціле число bi (0 ≤ bi ≤ K − 1), що позначає колір i-го блямблянчика і символ «L» (ліворуч) або «D» (праворуч) що позначають напрямок руху i-го блямблянчика. Усі цілі числа di будуть унікальними та заданими в строго зростаючому порядку. Програма виводить на пристрій стандартного виведення K рядків, i-й рядок містить загальний шлях блямблянчиків i–го кольору.
Приклади.
|
Введення 2 3 10 0 0 D 10 1 L
|
Виведення 10.0 10.0 0.0 |
Пояснення першого прикладу: блямблянчики стикаються через 5 метрів пройденого посередині палиці. Після цього обидва змінюють напрямок руху: той, що рухався вправо, після зіткнення забарвлюється в 0, тоді як той, що рухався ліворуч, після зіткнення, забарвлюється в 1.
|
|
Введення 4 3 7 1 0 D 3 0 D 4 1 L 6 2 D
|
Виведення 10.0 4.0 1.0 |
|
|
Введення 4 4 5 1 1 D 3 3 L 4 2 D 5 0 L |
Виведення 2.5 4.0 2.5 4.0 |
Задача Chip. Дошка для нашої гри складається з квадратів RхC. Рядки пронумеровані від 0 до R−1 зверху вниз, а стовпці від 0 до C−1 зліва направо. Кожна клітинка або сіра, або біла. Колір клітинки визначається так:
• білий, якщо номери рядка і стовпчика клітинки, представлені в двійковому вигляді, мають принаймні одну цифру 1 на тому самому місці. Наприклад, клітинка (4, 5) буде білою.
• сірий, якщо інакше. Наприклад, клітинка (2, 5) буде сірою.
На рисунку показана дошка розміром 10х0.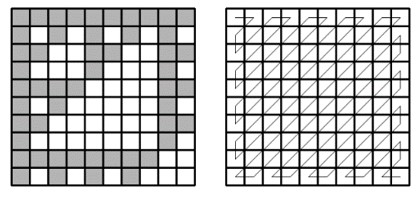
Фішка гравця ходить по дошці таким чином:
- починає шлях в клітинці (0, 0) і продовжує зигзагоподібно, як на другому зображенні вище. Відвідавши K клітинок за хід, фішка зупиняється. Допоможіть гравцю порахувати, в скількох сірих клітинках побувала фішка.
- Технічні умови. Програма Chip читає з пристрою стандартного введення з єдиного рядка цілі числа R (1 ≤ R ≤ 1 000 000), C (1 ≤ C ≤ 1 000 000) – розміри дошки, і ціле число K (1 ≤ K ≤ R·C) – загальну кількість квадратів, які відвідує фішка. Програма виводить на пристрій стандартного виведення кількість відвіданих сірих клітинок.
Приклади.
Введення
10 10 6
Виведення
5
Введення
3 5 11
Виведення
8
Введення
10 10 100
Виведення
51
Задача Train2021. У зв'язку з збільшенням кількості аварій на залізничній трасі керівництво залізничної компанії вирішило змінити графік руху поїздів. Ретельний аналіз стану полотна встановив, що оптимальним є наступний графік руху: спочатку T1 хвилин поїзд йде зі швидкістю V1 метрів за хвилину, потім T2 хвилин зі швидкістю V2 м/хв, …, нарешті, TN хвилин зі швидкістю VN м/хв. Протягом інтервалу Ti (1≤i≤N) поїзд може стояти.
За діючою інструкцією забезпечення безпеки руху відстань між головними вагонами поїздів, що проходять один за одним, ніколи не повинна бути менше L метрів. Напишіть програму, яка визначає мінімально допустимий інтервал у хвилинах між відправленнями поїздів, що дозволяє їм рухатися за встановленим графіком без небезпечного зближення.
Технічні умови. Програма Train2021 читає з пристрою стандартного введення у першому рядку натуральні числа, що задають мінімально допустиму відстань L і кількість ділянок шляху N (100≤ L≤ 10000, 1≤ N ≤ 1000). Далі слідують N пар цілих чисел T1, V1, …, TN, VN, що описують графік руху (1≤Ti≤1000, 0≤Vi≤1000).
Програма виводить потрібно вивести інтервал між відправленнями поїздів у хвилинах з максимально можливою точністю.
Приклад
Введення
1000 4
10 0
30 80
15 0
20 100
Виведення
27.5000000
Завдання підготували Г.Непомнящий, К.Сімонов, Ю.Пасіхов


