Завдання другого туру NetOI-2021
(розв'язки приймаються до 0 годин 31 грудня 2021 р.)
Задача Graph2021. У графа Михайла є n садиб, розташованих по колу. Він хоче побудувати кілька підземних переходів між садибами, щоб пересуватися між ними швидше. Ви можете вибрати якесь число k, таке, що для кожної садиби вона буде з'єднана з k сусідніми ліворуч і з k садибами справа. Яке ж мінімальне k ви повинні обрати, щоб найкоротша відстань між будь-якими двома садибами була не більшою d ? Відстань між двома садибами вимірюється кількістю переходів, які потрібно зробити, щоб дістатися з однієї садиби до іншої.
Технічні умови. Програма Graph2021 читає з першого рядка ціле число t (1≤t≤10) – число наборів вхідних даних. Для кожного набору вхідних даних на новому рядку вводиться два цілих числа n і d (3 ≤ n≤ 1012, 1 ≤ d≤ 1012).
Програма виводить на пристрій стандартного виведення для кожного набору вхідних даних одне число в новому рядку – мінімальне k, що задовольняє умову задачі.
Приклад
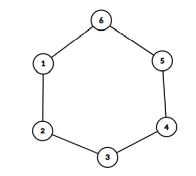
Коментар У першому наборі вхідних даних якщо ми з'єднаємо кожну садибу з кожним із сусідів, тобто якщо k = 1), то для попадання в протилежну садибу потрібно буде здійснити 3 переходи (див. рисунок)
|
 |
||||||
|
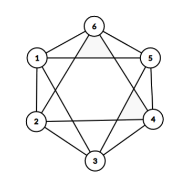
Якщо з'єднати кожну садибу з двома сусідами (к = 2) буде ситуація як на малюнку і знадобиться небільше двох переходів для потрапляння з будь-якої садиби до будь-якої. |
 |
||||||
Задача Parkur. Вам подарували гру, в якій паркурист стрибає по дахах хмарочосів. На кожному рівні гри генерується новий проспект з хмарочосів, де кожна висотка задається унікальною додатною координатою відносно початку проспекту. Після цього обирається будівля, з якої паркурист розпочинає свій шлях, при цьому він може стрибати тільки на будівлю, координата якої більша за поточну. Складність цієї гри полягає в тому, що після кожного стрибка герой втомлюється і вже не може стрибати так далеко як раніше. Формально кажучи, на кожному рівні генерується n будівель, координати яких рівні a1;a2;…;an. Гравець обирає стартовий хмарочос і з нього може стрибнути на будь-яку будівлю, яка знаходиться правіше, при цьому довжина першого стрибка може бути будь-якою. Для усіх подальших стрибків справедлива умова: якщо зараз гравець знаходиться на будівлі з координатою ai, а до цього був на позиції aj, то він може перестрибнути на будівлю з координатою ak, якщо ai-aj>ak-ai. Для кожного рівня знайдіть максимальну кількість хмарочосів, яку можна відвідати.
Технічні умови. Програма parkur читає з пристрою стандартного введення кількість будівель на даному рівні гри n (1≤n≤5000) і позиції цих будівель a1;a2;…;an (0≤ai≤1018; ai≠aj, якщо i≠j ). Гарантується, що сума n не перевершує 30000. Програма виводить на стандартний пристрій виведення максимальну кількість хмарочосів, яку можна відвідати.
Приклади
Введення
5 9 19 3 8 6
Виведення
4
Введення
3 16 5 17
Виведення
3
Коментар
У першому прикладі оптимальний вибір хмарочосів 3; 5; 4; 1, їхні координати 3; 6; 8; 9.
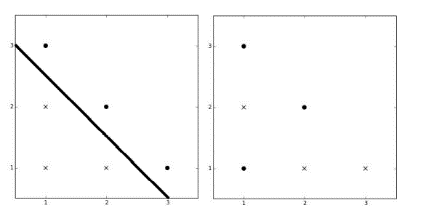Задача learning. У машинному навчанні часто виникає завдання лінійної класифікації об'єктів, коли класи об'єктів поділяються між собою лінійною поверхнею. Наприклад, у нас є інформація про кількість днів з моменту реєстрації облікового запису в соціальній мережі та кількість надісланих повідомлень за останній день, а також інформація про те, чи є цей обліковий запис спам-ботом. Вік облікового запису ми можемо взяти за X координату точки, а кількість повідомлень за Y координату. Завдання класифікації полягає в тому, щоб провести якусь пряму так, щоб об'єкти одного тину знаходилися але одну сторону цієї прямої, а об'єкти іншого тину та іншу.
За наявності такої прямої ми зможемо прогнозувати тип навіть незнайомого об'єкта але відомому віку облікового запису та кількості відправлених повідомлень залежно від того, з якого боку від прямої виявився об'єкт. Звичайно, у реальних даних можуть бути помилки вимірів або незвичайні об'єкти і провести таку пряму не всіх так можливо, тому що, наприклад, об'єкт першого тину може випадково потрапити в скупчення об'єктів другого типу і відокремити його прямо неможливо.
Вам необхідно за інформацією про параметри та тип об'єктів визначити, чи існує пряма, яка однозначно поділяє класи об'єктів. Пряма не повинна проходити ні через один об'єкт.
Технічні умови. Програма Learning читає з пристрою стандартного введення кілька тестових блоків. У першому рядку задано число Т - кількість тестових блоків (1 ≤ Т ≤ 100). Кожен тестовий блок складається з числа N - кількість описаних об'єктів (1 ≤ N ≤ 2000). У наступних N рядок міститься опис об'єктів, що складаються з трьох цілих чисел X, У, Туре (0 ≤ X, У ≤ 107, 0 ≤ Туре ≤ 1). Програма виводить на пристрій стандартного виведення для кожного тестового блоку YES, якщо поділ можливий і NO, якщо ні, для кожного блоку в окремій стрічці.
Приклад
|
Введення |
Виведення |
|||
|
2 |
|
|
|
YES |
|
6 |
|
|
|
NO |
|
1 |
1 |
1 |
|
|
|
1 |
2 |
1 |
|
|
|
1 |
3 |
0 |
|
|
|
2 |
1 |
1 |
|
|
|
2 |
2 |
0 |
|
|
|
3 |
1 |
0 |
|
|
|
6 |
|
|
|
|
|
1 |
3 |
0 |
|
|
|
2 |
2 |
0 |
|
|
|
1 |
2 |
1 |
|
|
|
3 |
1 |
1 |
|
|
|
2 |
1 |
1 |
|
|
|
1 |
1 |
0 |
|
|
Задача Toxins. У популярній настільній грі завдання полягає в тому, щоб провести фішку по певному маршруту. Поле є прямокутником, що складається з квадратних клітинок. Гравець може за один хід перейти в одну з чотирьох сусідніх по стороні клітинок, не виходячи при цьому за межі поля. Гравець починає свій шлях у будь-якій клітинці самого лівого стовпця і повинен потрапити до будь-якої клітинки самого правого стовпця ігрового поля.
Але окремі клітинки токсичні, їх розташування відоме. Вася з'ясував, що чим більша відстань від токсичної клітинки, тим безпечніший маршрут, відстань обраховується як кількість ходів клітинками токсичних клітинок до кожної клітинки маршруту. Допоможіть йому визначити, на яку мінімальну відстань доведеться підійти до токсичної клітинки, рухаючись найбезпечнішим маршрутом.
Технічні умови. Програма Toxins читає з пристрою стандартного введення першому рядку записано натуральні числа N та М (1 ≤ N,М ≤500) — кількість рядків та стовпців на ігровому полі, у другому рядку записано натуральне число К (1≤К≤500) — кількість токсичних клітинок. У наступних К рядок записані пари чисел Ri Ci (1≤ Ri ≤N, 1≤Ci≤ М) — координати токсичних клітинок (рядок, стовпець). Програма виводить на пристрій стандартного виведення мінімальну відстань, на яку доведеться наближатися до токсичної клітинки на безпечному маршруті.
Приклад
|
Введення |
Виведення |
Коментар |
|
10 10 4 2 2 5 3 5 9 8 8
|
3 |
Приклад одного з безпечних маршрутів показано на малюнку. Токсичні клітинки – чорні, клітинки маршруту – сірі. Мінімальна відстань між токсичною клітинкою та маршрутом – 3 ходи |
Задача Track2021. В на мапі країни Тракландія часина доріг, що з’єднують міста, заборонена лише для вантажного транспорту, а частина заборонена лише для велосипедистів, решта дозволена для всіх учасників руху Президент країни вирішив, що під час пандемії саме час ремонтувати та переробляти дороги. Потрібно закрити на ремонт якнайбільше доріг таким чином, щоб всі учасники дорожнього руху (легковики, велосипедисти, вантажівки, інше) могли з будь-якого міста потрапити в будь-яке інше, при чому, не порушуючи правил (тобто, не їдуть по забороненим дорогам).
Технічні умови. Програма Track2021 читає з пристрою стандартного введення число N (1£N£500) – кількість міст в країні, далі, через пропуск число M (1£M£10000) – кількість доріг. Далі йде M стрічок по 3 числа через пропуск в кожній. Перше та друге число в кожній трійці – номера міст, а третє число – тип дороги, що ці міста з’єднує.( 1-заборонено вантажівкам, 2- заборонено велосипедистам, 3- можна їхати всім). Між будь-якими двома містами існує не більше однієї дороги. Програма виводить на пристрій стандартного виведення кількість доріг, що закриваються. Якщо розв’язку немає, вивести -1
Приклад
|
Введення |
Виведення |
|
5 7 1 2 3 2 3 3 3 4 3 5 3 2 5 4 1 5 2 2 1 5 1 |
2
|
Завдання підготували Г.Непомнящий, Ю.Пасіхов