Задачі для учнів 9-11 класів
Задача Bank2021. Для прискорення обслуговування клієнтів у банку встановлено K кас. Упродовж дня банк обслуговує N клієнтів. Для кожного з клієнтів відомо, в який час він приходить і скільки часу займає його обслуговування. Коли клієнт приходить до банку, він отримує талончик із зазначенням номера каси, до якої йому слід підійти. Шлях від входу до каси номер 1 займає 1 секунду, до каси 2 – 2 секунди тощо. Стільки ж займає зворотний шлях від каси до виходу. Якщо каса, до якої підійшов клієнт, зайнята, він чекає своєї черги біля каси, і його обслуговування починається, як тільки каса звільниться. Напишіть програму, яка призначить касу кожному клієнту так, щоб він вийшов із банку якомога раніше. Якщо клієнта існує кілька варіантів вибору кас, слід призначити йому касу з найменшим номером.
Технічні умови. Програма Bank2021 читає з пристрою стандартного введення у першому рядку два натуральні числа N <=1000,і K<=10000 – кількість клієнтів і кас, відповідно. У наступних N рядках задаються пари натуральних чисел Si та Ti (S,T<=10000)– момент приходу та час обслуговування клієнта. Дані задані у порядку зростання часу приходу клієнтів; жодні два клієнти не приходять одночасно. Програма виводить на пристрій стандартного виведення N чисел через пропуск, де кожне з чисел задає номер каси, де повинен обслуговуватися клієнт. Виводити номери кас слід у порядку, в якому клієнти приходять до банку.
Приклад:
|
Введення |
Виведення |
|
3 2 1 10 3 6 4 1 |
1 2 1 |
Задача Graph2021.
У графа Михайла є n садиб, розташованих по колу. Він хоче побудувати кілька підземних переходів між садибами, щоб пересуватися між ними швидше. Ви можете вибрати якесь число k, таке, що для кожної садиби вона буде з'єднана з k сусідніми ліворуч і з k садибами справа. Яке ж мінімальне k ви повинні обрати, щоб найкоротша відстань між будь-якими двома садибами була не більшою d ? Відстань між двома садибами вимірюється кількістю переходів, які потрібно зробити, щоб дістатися з однієї садиби до іншої.
Технічні умови. Програма Graph2021 читає з першого рядка ціле число t (1≤t≤10) – число наборів вхідних даних. Для кожного набору вхідних даних на новому рядку вводиться два цілих числа n і d (3 ≤ n≤ 1012, 1 ≤ d≤ 1012).
Програма виводить на пристрій стандартного виведення для кожного набору вхідних даних одне число в новому рядку – мінімальне k, що задовольняє умову задачі.
Приклад
|
Введення |
Виведення |
|
2 6 2 3 1 |
2 1
|
Коментар
У першому наборі вхідних даних якщо ми з'єднаємо кожну садибу з кожним із сусідів (тобто якщо k = 1), то для попадання в протилежну садибу потрібно буде здійснити 3 переходи (див. рисунок)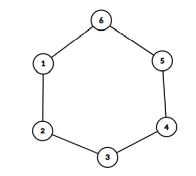
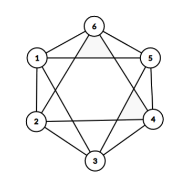
Якщо з'єднати кожну садибу з двома сусідами (к = 2) буде ситуація як на малюнку і знадобиться не більше двох переходів для потрапляння з будь-якої садиби до будь-якої.
Задача Parkur. Вам подарували гру, в якій паркурист стрибає по дахах хмарочосів. На кожному рівні гри генерується новий проспект з хмарочосів, де кожна висотка задається унікальною додатною координатою відносно початку проспекту. Після цього обирається будівля, з якої паркурист розпочинає свій шлях, при цьому він може стрибати тільки на будівлю, координата якої більша за поточну. Складність цієї гри полягає в тому, що після кожного стрибка герой втомлюється і вже не може стрибати так далеко як раніше. Формально кажучи, на кожному рівні генерується n будівель, координати яких рівні a1;a2;…;an. Гравець обирає стартовий хмарочос і з нього може стрибнути на будь-яку будівлю, яка знаходиться правіше, при цьому довжина першого стрибка може бути будь-якою. Для усіх подальших стрибків справедлива умова: якщо зараз гравець знаходиться на будівлі з координатою ai, а до цього був на позиції aj, то він може перестрибнути на будівлю з координатою ak, якщо ai-aj>ak-ai. Для кожного рівня знайдіть максимальну кількість хмарочосів, яку можна відвідати.
Технічні умови. Програма parkur читає з пристрою стандартного введення кількість будівель на даному рівні гри n (1≤n≤5000) і позиції цих будівель a1;a2;…;an (0≤ai≤1018; ai≠aj, якщо i≠j ). Гарантується, що сума n не перевершує 30 000. Програма виводить на стандартний пристрій виведення максимальну кількість хмарочосів, яку можна відвідати.
Приклади
Введення
5 9 19 3 8 6
Виведення
4
Введення
3 16 5 17
Виведення
3
Коментар
У першому прикладі оптимальний вибір хмарочосів 3; 5; 4; 1, їхні координати 3; 6; 8; 9.


