ЗАВДАННЯ 3-ГО ТУРУ NetOI-2020 (26 січня 2021 - 10 лютого 2021 р.)
Задача DIFF
“Вундеркінд” Сергійко на уроці математики придумав для сусіда гру. Записавши в ряд N цілих чисел x1,x2,…,xN, він запропонував замінити якусь пару чисел xk,xk+1, що стоять поруч, їхньою різницею xk-xk+1 (завжди віднімаємо з першого числа друге, але не навпаки). Потім він повторював цю дію доти, доки не залишиться одне число. Яке максимальне число M можна отримати таким чином?
Технічні умови. Програма DIFF читає з стандартного пристрою введення з першого рядка кількість чисел N(1<N≤10000), з наступних N рядків числа x1,x2,…,xN (-10000≤xk≤10000,k=1,2,…,N). Програма виводить на пристрій стандартного виведення шукане число M.
Приклад.
|
Введення 3 1 2 3 |
Виведення 2
|
Задача AGENTS.
Відділ доставки фірми «Роги і Копита» обслуговує торгові точки. Щодня товар завозиться в одну з них. Графік завезення по днях складено заздалегідь, причому в цьому графіку точки можуть повторюватися.
Два агенти з машинами розподілили замовлення між собою. Щодня один з них завозить товар в чергову торгову точку і залишається в ній, а другий нікуди не переміщується. Робота агентів спланована так, щоб сумарні витрати пального були мінімальними. Торгові точки задано своїми координатами. З точки в точку агенти переміщуються по прямій. Перед початком роботи агенти знаходяться в точці площини з координатами (0,0). Знайдіть сумарний пробіг машин S.
Технічні умови. Програма AGENTS читає з першого рядка кількість торгових точок N (1,1<N≤10), далі з наступних N рядків N пар дійсних чисел (x1,y1),(x2,y2),…,(xN,yN) — координати 1-ої, 2-ої, …, N-ої торгових точок (-1000.0≤xk,yk≤1000.0,k=1,2,…,N), з наступного рядка кількість днів у графіку M(1<M≤10000), з наступних M рядків числа K1,k2,…,kM(1≤Kj≤N,j=1,2,…,M)— номери точок, які треба відвідати в 1-й, 2-й, …, M-й день. Програма виводить на пристрій стандартного виведення сумарний пробіг машин S з точністю до 10-5.
Приклад.
|
Введення 3 3.0 4.0 1.0 4.0 4.0 1.0 5 2 3 1 3 2 |
Виведення 12.2462112512
|
Задача BARREL.
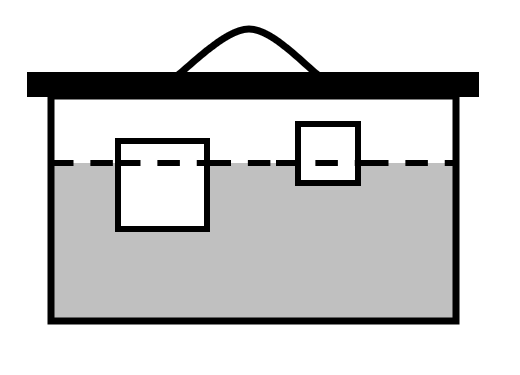
Є бочка з деякою кількістю води. У бочку опускають задану кількість брусків у формі куба різних розмірів і густини. Потім згори опускають кришку так, що вона торкається країв бочки. Треба визначити отримуваний рівень води. Передбачається, що густина води дорівнює 1.0; присутність повітря можна не враховувати; усі бруски цілком влізають у бочку; бруски розташовуються у воді вертикально і не торкаються один одного.
Технічні умови. Програма BARREL читає з клавіатури з першого рядка три дійсні числа - площу дна бочки S (0<S≤1000.0), висоту бочки H (0<H≤1000.0), об'єм води V (0<V≤SH), з наступного рядка кількість брусків N (0<N≤1000), і далі з наступних N рядків N пар дійсних чисел - довжини сторін кубів Lk (0<Lk≤1000.0) і їх густини Dk (0<Dk≤10.0), k=1,2,…,N. Програма повинна вивести на екран дійсне число - рівень води у бочці після додавання брусків. Це число треба визначити з точністю до 10-4.
Приклад
|
Введення 100.0 10.0 500.0 1 1.0 0.5
|
Виведення 5.0050
|
|
Задача COOKIES.
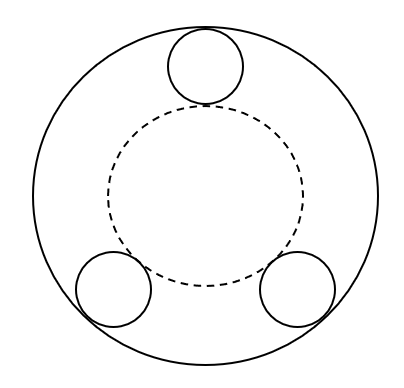
Бабуся готувала печиво. Для цього вона розкотила тісто у великий пласт у формі круга і скляночками різних діаметрів видавила в ньому круглі шматочки, щоб потім запекти їх і отримати з них смачне печиво. Відомо, що жодні два круглі вирізи не перетинаються між собою, крім того, усі вирізи повністю містяться всередині пласта. Проте вирізи можуть торкатися один одного і краю пласта. Улюблений онук з корисливих міркувань вирішив допомогти бабусі: він вирішив видавити в частині пласта, що залишилася, круглу заготовку для печива якомога більшого розміру. Проте він не знає, який діаметр має бути у скляночки, якою треба видавлювати таку заготовку. Допоможіть йому.
Технічні умови. Програма COOKIES читає зі стандартного пристрою введення з першого рядка радіус пласта R (1<R≤1000.0). Відомо, що центр пласта знаходиться в точці (0,0). З другого рядка програма читає натуральне число N (1≤N≤100) – кількість вирізаних заготовок. З наступних N рядків програма читає положення і радіуси вирізаних заготовок - дійсні числа, розділені пропуском. Програма виводить до стандартного пристрою виведення радіус максимальної за розміром заготовки, яку ще можна вирізати з цього пласта. Відповідь не повинна відрізнятись від правильної більше, ніж на 10-3.
Приклад
|
Введення 1.01 3 0.0 0.83333 0.166667 0.72169 -0.416667 0.166667 -0.72169 -0.416667 0.166667 |
Виведення 0.666666 |
|
Задача TRIANG
Триангуляцією опуклого многокутника називається розбиття його на трикутники діагоналями, що попарно не перетинаються. Степінню вершини відносно заданої триангуляції будемо вважати кількість діагоналей, які виходять з цієї вершини.
Дано правильний N-кутник. Перенумеруємо всі його вершини у порядку обходу проти годинникової стрілки натуральними числами від 1 до N. Нехай дано невід’ємні цілі числа d1, d2, …, dN. Потрібно визначити, чи існує хоча б одна така триангуляція, що для усіх i від 1 до N вершина i має відносно неї степінь di, і якщо існує, вказати будь-яку з них.
Технічні умови. Програма TRIANG у першому рядку читає з клавіатури ціле число N (3≤N≤200000), у другому – N цілих чисел d1, d2, …, dN (0≤di≤N). Програма виводить на екран К – кількість діагоналей, які задають шукану триангуляцію, а далі – K рядків з діагоналями. Кожна діагональ задаєтся двома числами – номерами вершин, які нею з’єднуються. Кожна діагональ повинна виводитися у окремому рядку. Номери вершин розділяються одним пропуском. У випадку, якщо триангуляції із заданими степенями вершин не існує, виведіть одне число -1.
Приклад
|
Введення |
Виведення |
|
6 1 0 2 1 0 2 |
3 1 3 3 6 4 6 |
|
Введення 5 2 0 2 0 2 |
Виведення -1 |
Завдання підготували Г.непомнящий , Ю.Пасіхов