Завдання ІІІ туру NetOI-2018.
Розв’язки приймаються до 0 годин 26 січня 2019 р.
Задача Typo. На комп’ютерах серії “Буг” кожна літера задається матрицею у N рядківта M стовпчиків, кожен піксель якої або чорний, або білий. Введемо поняття кернінгу між сусідніми символами. Кернінгом назвемо суму відстаней (тобто кількість білих пікселів) між найлівішим чорним пікселем правої літери і найправішим чорним пікселем лівої літери по кожному рядку. До прикладу, нехай N = M = 3 і ми розглядаємо два сусідні символи: У даному випадку у першому рядку відстань рівна 1, у другому 2, утретьому 1, тож сумарно маємо 4, а отже і кернинг буде 4. Вам дані 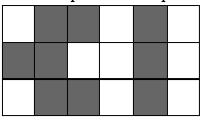
нариси N символів (причому кожен символ містить хоча б один чорний піксель у кожному рядку). Потрібно визначити, чи можна з них скласти послідовність (можливо, з повторами) так, щоб сума кернінгів між усіма
парами сусідніх літер складала рівно X. В порожнього рядку сумою кернінгів буде 0. Оскільки це дуже важлива задача, ми попросимо вивести відповідь для багатьох запитів.
Технічні умови. Програма Typo читає з пристрою стандартного введення 3 цілих числа N, M, K (1 ≤ N, M, K ≤ 100) - розміри матриці, що задають кожен символ та кількість символів. Далі слідують K*N рядків по M символів, причому кожні N послідовних рядків задають нарис певного символа. “#” (символ решітки) при цьому означає чорний піксель, ‘.’ (символ крапки) - білий. Далі слідує число Q (1<=Q<=100) -кількість запитів, після чого слідують Q цілих невід’ємних чисел (кожне не перевищує 109) - власне, запити. Програма має вивести рівно Q символів “Y” у випадку, якщо навідповідний запит відповідь “так” (тобто можна скласти послідовність з символів відповідним кернінгом) або “N” у іншому випадку.
Приклад
Введення
3 3 2
.##
##.
.##
.#.
.#.
.#.
3
4 5 2
Виведення
YYN
Задача Travel2018. У великому місті всі мешканці їздять лише автобусами. Жителі вимушені витрачати час, економлячи гроші - одноразові квитки дорогі. Тому пасажири намагаються планувати поїздки так, аби пересідати з маршруту на інший як можна меншу кількість разів. Добре, що в місті на кожній зупинці висить розклад руху автобусів по всім маршрутам. Напишіть програму, яка допоможе доїхати з однієї вибраної зупинки на іншу, використовуючи мінімальну кількість одноразових квитків.
Технічні умови. Програма Travel2018 читає з стандартного пристрою введення у першому рядку чотири цілих числа, розділені пропусками: кількість автобусів N, кількість зупинок у місті M, число A – зупинка, де пасажир починає поїздку і число В - зупинка, куди хоче доїхати пасажир. Автобуси нумеруються від 1 до N, зупинки - від 1 до M ( 1 ≤ N ≤ 1000; 1 ≤ M ≤ 1000; 1 ≤ A, B ≤ M; A ≠ B.) Наступні М рядків містять списки зупинок автобусів. (i +1) -й рядок описує i-ту зупинку: перше ціле число Li (1 ≤ Li ≤ N) - кількість автобусів, що зупиняються на ній, а далі Li цілих чисел, розділених пропусками - номери маршрутів цих автобусів. Гарантується, що розв’язок існує. Програма виводить на стандартний пристрій виведення одне ціле число K - мінімальна кількість одиночних квитків, щоб доїхати від А до B
Приклад
Введення
4 9 1 8
2 1 2
2 2 3
1 1
3 1 2 3
1 3
2 3 4
1 3
1 4
1 2
Виведення
3
Коментар. Сідаємо в автобус №2,їдемо до зупинки 2, потім на автобусі №3. їдемо до зупинки 6 і на автобусі № 4 доїжджаємо зупинки 8. Це не єдиний спосіб досягти мети, використовуючи лише 3 одноразові квитки.
Задача Cezar. Над рядком з N літер латинського алфавіту трішки познущалися. Спершу пронумерували усі суфікси від 1 до N, починаючи зліва направо. Наприклад, у рядку “abc” суфікс “abc” - перший, суфікс “bc” - другий, суфікс “c” - третій. Далі відсортували суфікси у алфавітному (лексикографічному) порядку. Після цього усі суфікси замінили на їх номери. Отриману послідовність назвемо характеристичною для цього рядка.
На жаль, початковий рядок було втрачено, але на щастя, залишилась характеристична послідовність і інший рядок з N літер латиниці. Крім того, у вашому розпорядженні наявний шифратор. Цей автомат приймає на вхід два рядки - один з N літер (джерело), інший рівно з 26 літер (ключ). Шифратор заміняє усі входження літери “a” у джерелі на першу літеру з ключа, усі входження літери “b” на другу літеру ключа (загалом усі входження i-тої літери латиниці у джерелі на i-тий символ у ключі). Необхідно віднайти такий ключ з 26 літер, який би у парі з даним в умові джерелом з N літер давав рядок з даною характеристичною послідовністю. При цьому шуканий ключ має бути перестановкою літер латинського алфавіту, тобто кожна літера повинна зустрічатися там рівно один раз.
Технчічні умови. Програма Cezar читає з пристрою стандартного введення натуральне число N (що не перевищує 100000) - кількість символів у вхідному рядку. З другого рядку програма має читати перестановку з N натуральних чисел - характеристичну послідовність. У третьому рядку рівно N маленьких символів латиниці - джерело.
Програма виводить на пристрій стандартного виведення рівно 26 символів латиниці у разі, якщо існує деякий ключ, який міг би у парі з джерелом при перетворенні у шифраторі дав би рядок, характеристична послідовність якої вказана у другому рядку вхідних даних. Якщо таких ключів декілька, виведіть лексикографічно мінімальний. Якщо жодного можливого ключа немає, виведіть IMPOSSIBLE.
|
Введення |
Виведення |
|
3 1 2 3 aaa |
IMPOSSIBLE |
|
Введення |
Виведення |
|
3 1 2 3 cba |
cbadefghijklmnopqrstuvwxyz |
Коментар до другого прикладу: при заміні літера “a” перейде в “c”, літера “b” перейде сама у себе, а літера “c” перейде в літеру “a”. Відповідно, за лексикографічним порядком, “abc” < “bc” < “c”, тобто суфікси відсортовані як 1 2 3.
Задача Lib2019 У пошуках задач для третього туру олімпіади NetOI-2018 два члени журі вирішили відвідати приміщення, де зберігаються паперові архіви старих олімпіад «догуглівської» епохи. Архів розміщений у просторій залі у формі багатокутника без самоперетинів (але не обов’язково опуклий). Колеги вирішили, що безпечніше буде не втрачати одне одного з поля зору. На якій максимальній відстані можуть знаходитися колеги, щоб не втрачати одне одного з поля зору і не виходити за межі архіву? Члени журі бачать одне одного, якщо між ними можна провести відрізок, жодна з точок якого не лежала б ззовні архіву.
Технічні умови. Програма Lib2019 читає з клавіатури число N (3 ≤ N ≤ 300) кількість вершин багатокутника. Далі слідують N пар цілих чисел (кожне з яких не перевищує 1000 за абсолютною величиною) - координати вершин багатокутника в порядку обходу за або проти годинникової стрілки. Багатокутник не має ні самоперетинів, ні самодотиків. Програма має вивести єдине число - відповідь на задачу з точністю не менш як 5 знаків після коми.
Приклад
|
Введення |
Виведення |
|
4 2 2 2 3 3 3 3 2 |
1.414213 |
Задача Words2018. Квадратна таблиця розмірів NxN заповнюється великими літерами латинського алфавіту Першу літеру алфавіту вставляють у будь-яку вільну клітинку, потім другу і т.д. Після останньої літери алфавіту (якщо є ще порожні клітинки), літери знову починаються від початку алфавіту. Данo слово. Напишіть програму, яка буде знаходити маршрут у таблиці від верхнього лівого поля до правого нижнього, де кожна літера з даного слова з'явиться на шляху хоча б один раз. Порядок літер на маршруті не має значення. Довжина маршруту (кількість відвіданих клітинок, включно х початковою та кінцевою) повинна бути мінімальною. Якщо клітинка кілька разів входить до маршруту, то вона підраховується стільки ж разів. Можливо переходити з одної клітинки в іншу, якщо вони мають спільну сторону, але не можна переходити «знизу вгору», тобто не можна повернутися на попередній рядок. Гарантується, що розв’язок завжди існує.
Технічні умови. Програма Words2018 читає з пристрою стандартного введення ціле число N у першому рядку - це розмір таблиці, у другому - слово, яке ми
|
Приклад |
|
|
Введення 6 VAIVA IKHJQL ETEFGH WXUVCY MIABFG AOBCSD ZNJPRD |
Виведення 13
|
шукаємо. N>5, K>0, N*K≤ 81. тут K - кількість букв у слові. Далі програма читає таблицю літер у наступних N рядках. Кожний рядок містить N літер без пропусків. Передбачається, що рядки нумеруються (починаючи з одиниці) згори вниз, стовпці (починаючи з одиниці) - зліва направо. Програма виводить на пристрій стандартного виведення єдине число – мінімальну довжину шляху. Сам шлях виводити не потрібно.
Завдання підготували Г.Непомнящий, Ю.Пасіхов, М.Стречень


