Задача Soldier. У деякій (здогадайтесь самі, у якій) войовничій країнi солдати-призовники роблять дві справи: - фарбують травичку та ходять строєм. I якщо з фарбуванням все легко, то стройова підготовка потребує багато часу та сил, особливо за умов, коли ось-ось черговий військовий парад...
Плац, по якому крокуватимуть солдати нашого героїчного взводу, являє собою прямокутник N×M(2≤N,M≤700) (якщо прийняти розмір «коробки» взводу солдат за квадрат з одиничною стороною), деякі клітинки якого зайняті іншими підрозділами, тож взводу ходити через цi клітинки забороняється. Відомі також початковий та кінцевий пункти руху взводу. Сержант Pupkin добре знає - солдати відмінно ходять по прямій, а ось команди «наліво», «направо» i «кругом» виконують іноді з помилками, тож він хоче, щоб на святковому проходженні взвод зробив якомога менше поворотів. Допоможіть сержанту знайти маршрут з найменшою кількістю поворотів.
Технічні умови. Програма Soldier читає з пристрою стандартного введення у першому рядку N - кількість рядків у схема плацу. У другому рядку M - кількість стовпчиків. Далі N рядків по M символів у кожному. Символ «.» означає вільну клітинку, символ «X» зайняту. Також існує рівно один символ «S» та один символ «F», що позначають відповідно початкову та кінцеву точки проходу взводу. Хоча б один маршрут між S та F завжди існує.
Програма виводить на пристрій стандартного виведення єдине число - мінімальну кількість поворотів взводу на маршруті. Перед початком маршу сержант може вишикувати взвод обличчям у будь-яку сторону – як йому це зручно.
| Приклад | |
|
Введення 3 |
Виведення 1 |
Задача Binfriend. Для натурального числа N назвемо бінарним другом число вигляду 2t+1 (t - натуральне), що ділиться націло на N. Вам необхідно знайти найменше число з бінарних друзів чи констатувати відсутність таких для кожного з чисел заданого набору.
Технічні умови. Програма Binfriend читає з пристрою стандартного введення число M(1≤M≤100) - кількість чисел у наборі, і в тому ж рядку рівно M натуральних чисел, кожне з яких не перевищує 1015. Програма виводить на пристрій стандартного виведення в одному рядку через пропуски M чисел - мінімальне ціле невід’ємне t таке, що Ni ділить 2t +1 націло. Якщо такого немає, слід вивести -1.
| Приклад | |
|
Введення 3 1 4 11 |
Виведення 0 -1 5 |
Пояснення до прикладу:
Для 1, очевидно, мінімальним t буде 0. Оскільки жодне число вигляду 2t +1 за t>1 не може бути парним, то жодне не зможе i ділитися на 4. Для 11 за t = 5 маємо друга 25 +1 = 33.
Задача Maxtriangle. Цензура в геометричному світі! Багатокутники з кількістю сторін, що більша за 3, під забороною. У зв’язку з цим усі багатокутники намагаються перетворитись на трикутники (іноді вироджені). Роблять це вони у такий спосіб: поки кількість сторін не дорівнює 3, обираються дві суміжні сторони, що об’єднуються в одну, довжина якої дорівнює сумі довжин об’єднаних. Кожному багатокутнику цікаво, якою буде його максимально можлива площа після «трикутизацiї». Допоможіть їм у цьому!
Технічні умови. Програма Maxtriangle читає з пристрою стандартного введення число N(3≤N≤7000) - кількість сторін опуклого багатокутника. В цьому ж рядку слідує N натуральних чисел, кожне з яких не перевищує 105 - розміри сторін (сторони задаються у тій послідовності, у якій вони були в багатокутнику). Гарантується, що периметр багатокутника не перевищує 70000. Програма виводить на пристрій стандартного виведення єдине дійсне число - максимальну площу багатокутника після «трикутизацiї». Відповідь буде зарахована, якщо відносна чи абсолютна похибка не перевищує 10−5 від відповіді журі.
| Приклад | |
|
Введення 4 1 2 3 4 |
Виведення 4.472136 |
Задача Trees2018. Робот-провідник моделі TouristVasya призначений для організації туристичних походів лісами Поділля. Нещодавно у ньому знайшли проблему - у деяких ситуаціях робот може заблукати в чотирьох соснах. Працівники туристичної компанії, яка купила робота, вже зрозуміли алгоритм, за яким робот обходить перешкоди: натикаючись на дерево, робот повертає на 90 градусів праворуч, після чого йде прямолінійно до наступної зустрічі з деревом (або поки не вийде з лісу). На жаль, виправлення помилок програмного забезпечення - справа довготривала i дорога, тож туристична компанія вирішила знайти усі проблемні маршрути i видати відповідні брошури з рекомендаціями туристам. Проблемним маршрутом назвемо замкнену послідовність обходу роботом чотирьох дерев, при цьому робот жодним чином (рухаючись за алгоритмом) вийти з цього маршруту не може. Вам доручається розробити програму, яка б за мапою дерев визначила б кількість проблемних маршрутів. Маршрути вважаються різними, якщо відрізняється четвірка дерев, що входить у цей маршрут. До прикладу, четвірки (1,2,3,4) та (3,2,1,4) однакові, у той час як (1,2,3,5) та (1,5,4,3) - різні.
Технічні умови. Програма Trees2018 читає з пристрою стандартного введення в першому рядку ціле число N(1≤N≤1000) - кількість дерев на мапі. В наступних N рядках координати дерев у форматі xiyi. При цьому кожна з координат не перевищує 109 за абсолютною величиною. Жодних два дерева не розміщені в одній точці. Жодних три дерева не розміщені на одній прямий. Програма виводить на пристрій стандартного виведення єдине число - кількість проблемних маршрутів.
Приклади
|
Введення |
Виведення |
Введення |
Виведення |
|
8 1 0 0 1 -1 0 0 -1 2 2 2 4 4 2 4 4 |
2 |
8 1 2 2 1 -1 2 -2 1 1 -2 2 -1 -1 -2 -2 -1 |
6 |
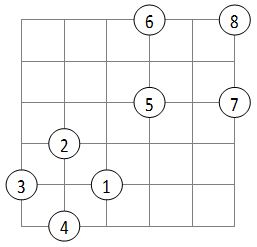
Пояснення до прикладів:
Проблемні маршрути такі:
- 3 → 2 → 1 → 4 → 3,
- 5 → 6 → 8 → 7 → 5,
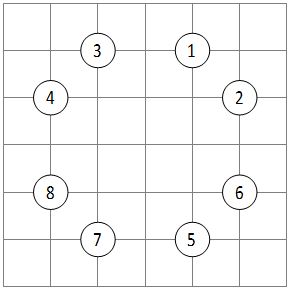
Проблемні маршрути такі:
- 3 → 1 → 5 → 7 → 3,
- 3 → 2 → 5 → 8 → 3,
Задача Islands. Є n островів, які пронумеровані від 0 до n-1. На нульовому острові знаходиться відомий мореплавець Гама-да-Васко. Йому відомо, що з кожного острова можна потрапити напряму лише на один інший, тобто з острова і можна потрапити лише на острів ai. Тому, щоб потрапити на якийсь острів, потрібно відвідати деякі інші, а на якісь острови взагалі потрапити неможливо. Мореплавець хоче відвідати якомога більше островів. Для цього він може змінити значення будь-якого ai. Скільки різних островів Гама-да-Васко зможе відвідати, якщо він може змінити шлях з будь-якого острова?
Технічні умови. Програма Islands читає з пристрою стандартного введення число n(1≤n≤2·105) - кількість островів, а далі n чисел ai(-1≤ai<n) - острів, на який веде шлях з острова i, якщо ai=-1, то з цього острова немає шляху. Програма виводить на пристрій стандартного виведення єдине число - максимальну кількість різних островів, які можна відвідати.
Приклади
| Введення | Виведення |
|
10 2 5 4 4 -1 1 -1 3 0 8 3 0 0 0 |
5 2 |
Завдання підготували В.Бездушний, А.Зуєв, Г.Непомнящий, Ю.Пасіхов, М.Стречень, А.Ципко


