РОЗВ'ЯЗКИ ПРИЙМАЮТЬСЯ ДО 00:00 27.01.2018
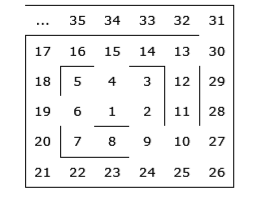
Задача Hoard. Пірати заховали ск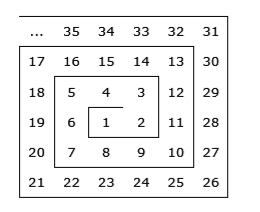
арб в підземному лабіринті, який складається з нескінченної кількості кімнат з кам'яними стінами. Кімнати мають номери і з'єднані переходами, так що все підземелля, якщо дивитись згори, виглядає як спіраль. Кімнати пронумеровані, як на малюнку. Після великого землетрусу деякі стіни зруйнувалися, а між суміжними кімнатами утворилися нові проходи. Вхід до лабіринту знаходиться в кімнаті 1. Шукач скарбів знає, що скарб знаходиться в кімнаті N. Напишіть програму, яка, враховуючи розташування скарбу N та список нових переходів, визначає найменшу кількість переходів, крізь які повинен пройти шукач, поки дістанеться до скарбу.
Технічні умови Програма Hoard читає з пристрою стандартного введення у першому рядку ціле число N (1 ≤ N ≤ 1015) - номер кімнати, в якій розташований скарб, у другому рядку - ціле число K (1 ≤ K ≤ 100 000), кількість нових переходів. Кожен з наступних K рядків містить одне ціле число B (4 ≤ B ≤ 1015), що означає, що тепер новий перехід об'єднує суміжні приміщення A та B, де A <B. Номер А не задано явним чином, але його можна однозначно визначити з B (наприклад, якщо B дорівнює 20, то A має бути 7). Крім того, в деякі кімнати ніколи не можуть бути номером В (номери 2, 3, 5, 7, 10, 13 тощо). Програма виводить на пристрій стандартного виведення єдине ціле число - найменшу кількість переходів, крізь які шукач повинен пройти, перш ніж він може дістатися до скарбу.
Приклади
|
Введення 31 9 15 25 30 6 9 19 24 27 4
|
Виведення 6 |
Введення 10000 5 52 4 9 25 27
|
Виведення 9953 |
Пояснення до першого прикладу: 1-4-15-14-13-30-31
До скарбу можна дістатися, пройшовши 6 проходів |
_________________________________________________________________________________________________
Задача Cool2k17. Назвемо число «крутим», якщо у його десятковому запису присутнi лише цифри 0, 1, 2. Перестановка чисел A1,A2,...,An лексикографiчно менша за перестановку B1,B2,...,Bn, якщо iснує k таке, що для усiх i < k справедливо Ai = Bi та для Ak < Bk. Вам дано число N - довжина перестановки (кiлькiсть чисел у перестановцi), а також число K - номер перестановки серед усiх перестановок, вiдсортованих лексикографiчно. Вам необхiдно знайти кiлькiсть «крутих» чисел, що стоять на «крутих» мiсцях, тобто їх iндекси в перестановцi також є «крутими» числами. Елементи в перестановцi нумеруються з 1.
Технiчнi умови. Програма cool2k17 зчитує з клавiатури два числа N та K, обидва не бiльшi за 1018. Програма повинна вивести єдине число - вiдповiдь на задачу. У разi, якщо K-ої перестановки не iснує, слiд вивести −1.
Приклади:
|
Введення |
Виведення |
|
3 12 |
-1 |
|
3 4 |
1 |
Коментар:
Усього існує 6 перестановок чисел вiд 1 до 3. Це (1;2;3),(1;3;2),(2;1;3),(2;3;1),(3;1;2), (3;2;1). Тому на перший приклад вiдповiдь −1 (12-ої перестановки не iснує). На другий приклад вiдповiдь 1 - у перестановцi (2;3;1) лише «круте» число 2 стоїть на «крутому» мiсцi 1.
-------------------------------------------------------------------------------------------------------------------------------------------
Задача Segtree2k17. В середовищі крутих олімпіадних гуру модно знати напам’ять розв'яок такої задачі: Дано масив з N чисел та M запитів виду L R. На кожен такий запит потрібно вивести добуток елементів масиву, що мають індекси від L до R, включно. Оскільки, добуток може бути дуже великим, вам потрібно виводити відповідь по модулю.
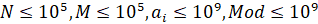
Розглянемо таку модифікацію цієї задачі: Умова задачі не змінюється, але змінено обмеження:
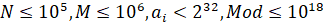
Оскільки, в такому випадку вхідний файл буде дуже великим, його пропонується генерувати. Код генератора (С++) повинен бути вбудований в розв’язок. (Аналогічний код мовами Pascal та Python 2* , 3* можна завантажити тут).
const int MAXN = 1000 * 1000;
long long a[MAXN];
long long mod;
unsigned s;
unsigned getNext(){
s ^= (s << 13);
s ^= (s >> 17);
s ^= (s << 5);
return s;
}
int main() {
unsigned n, m, seed ;
cin >> n >> m >> mod >> seed;
s = seed;
for(int i = 0; i < n; i++){
a[i] = getNext();
}
long long ans = 0;
for(int i = 0; i < m; i++){
unsigned left = getNext() % n;
unsigned right = getNext() % n;
if(left > right) swap(left, right);
long long result = query(left, right);
ans = (ans + result) % mod;
}
}
Таким чином , вхідними даними будуть N, M, Mod, Seed, де Seed – початкове значення для генератора. У відповідь потрібно вивести суму відповідей на кожен запит (по модулю)
Технічні умови. Програма Segtree2k17 (яка містить вбудований код генератора!) читає з пристрою стандартного введення натуральні числа N, M, Mod, Seed (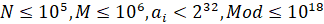 
seed<=232) Програма виводить до пристрою стандартного виведення єдине число – суму результатів (по модулю) на всіх запитах.
Приклади
Введення Виведен
10 15 1000000007 1 216091399
Введення Виведення
5000 100000 1283189389247 8932 541836623127
Введення Виведення
padding:0cm 0cm 1.0pt 0cm">1000 100 100007 7632 47019
______________________________________________________________
Задача Viability. Василь Пупенко (учасникам NetOI з кінця 1990-х років відомий як Вася Пупкін) захищає дисертацію з теорії чисел. Більше того, ввів в цю теорію кілька нових понять. Серцем цілого додатного числа він назвав добуток всіх десяткових цифр цього числа. Наприклад, серцем числа 2612 буде 2 · 6 · 1 · 2 = 24. А ось життєздатність такого числа - це добуток числа на його серце. Наприклад, життєздатність числа 2612 становить 2612 · 24 = 62688. Темою дисертації на здобуття ступеню Ph.D Василя стало дослідження: скільки є таких натуральних чисел, життєздатність яких лежить в проміжку від А до В? Допоможіть вченому - напишіть програму, яка порахує цю кількість, тим самим підтвердить Василеву теорію.
Технічні умови. Програма Viability читає з пристрою стандартного введення два цілих числа A і B (1 ≤ A ≤ B <1018) через пропуск к одному рядку. Програма виводить на пристрій стандартного виведення єдине число – шукану величину.
|
Введення 20 30 |
Виведення 2 |
|
145 192 |
4 |
|
2224222 2224222 |
1 |
Пояснення до другого прикладу. Життєздатності чисел 19, 24, 32 і 41 мають значення 171, 192, 192 і 164.
____________________________________________________________________________________________
Задача Vinsoft В м. Вінниця є N фірм, що займаються розробкою програмного забезпечення. Відомий вінницький олігарх Чайник вирішив монополізувати галузь в місті, створивши концерн Vinsoft. Для цього він вирішив придбати як можна більше фірм . Він розіслав відповідні пропозиції всім N компаніям і через деякий час отримав від кожної з них згоду або відмову. Але, як досвідчений бізнесмен, Чайник знає, що в бізнесі дуже багато залежить від взаємної довіри партнерів.
Шляхом збирання інформації Чайник виявив, між якими фірмами існує взаємна довіра (причому, завжди, якщо фірма A довіряє фірмі B, то фірма B довіряє фірмі A).
Тепер Чайник може повторно розіслати пропозиції всім фірмам, включивши до листа список фірм, що погодилися на його проект. При цьому кожна фірма, незалежно від своєї початкової позиції, дає згоду, якщо в списку є хоч одна фірма, якій вона довіряє, і відмовляється в іншому випадку. Таким чином, деякі фірми, які спочатку не погоджувались, тепер дають згоду «продатися» Чайнику, а деякі із тих, що спочатку дали згоду, відмовляються. В результаті у Чайника формується новий список, який він знову може розіслати фірмам. Таку операцію Чайник може повторювати багато разів, щоразу розсилаючи поточний список. Він може припинити процес в любий момент і придбати ті фірми, які після останнього розсилання погодилися. Яке максимальне число фірм може купити Чайник ?.
Як це не дивно, Чайник – чесний олігарх і ніколи не «підтасовує» списки .
Технічні умови. Програма Vinsoft читає з пристрою стандартного введення у першому рядку число N — кількість фірм (1≤N≤2000). Далі в тому ж рядку N чисел, що описують відповідь фірми на першу пропозицію Чайника (1 — згода, 0 — відмова). Далі - число M (0≤M≤200000) — кількість пар компаній, між якими існує довіра. Далі - M пар чисел, що задають номери фірм, між якими існує взаємна довіра (числа в парі не можуть бути однаковими). Будь-яка пара фірм згадується в списку не більше одного разу. Всі числа розділено пропусками. Програма виводить на пристрій стандартного виведення — максимальне число фірм, які зможе купити Чайник.
Приклади
|
Введення |
|
7 1 0 0 0 0 0 1 6 1 2 1 3 1 4 4 5 5 6 2 5 Виведення 4 |
|
Введення 3 0 0 0 0 Виведення 0 |
Завдання підготували В.Бездушний, Г.Непомнящий, Ю.Пасіхов, М.Стречень