G2048
У свій вільний час Гаррі Поттер з друзьями дуже полюбляють грати в інтелектуальні ігри і Герміона принесла їм нову гру. Її поле для гри має форму квадрата розміром 4х4. Перед першим ходом гри в деяких двох різних довільно обраних клітинках знаходяться плитки номіналу «2». Далі на кожному ході у довільно обраній вільній клітинці з’являється нова плитка номіналу «2». Натисканням стрілки гравець може зсунути всі плитки ігрового поля в одну з чотирьох сторін (уверх/вліво/униз/вправо). Якщо при виконанні дві плитки одного номіналу «налітають» одна на одну, вони зливаються в одну, номінал якої дорівнює сумі злитих. Наприклад, якщо дві плитки з номіналом «2» налетіли одна на одну, вони заміняються на одну плитку з номіналом «4» (2+2). При цьому ігрові бали збільшуються на номінал нової створеної плитки (у даному випадку на 4). За один хід може виконатися кілька операцій злиття і в цьому випадку всі бали додаються. Наприклад, розглянемо такий стан гри:
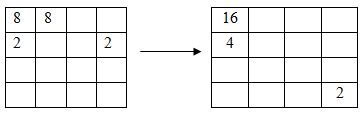
Зсув вліво у цьому випадку додає дві «2» та дві «8» і дає 4+16=20 очок.
Після цього у довільній вільній клітинці з’являється 2.
Гаррі почав грати у запропоновану гру, але чергові події, пов’язані з відкриттям Таємної кімнати, відволікли його у самий розпал гри. Не довідавшись нічого нового, Гаррі повернувся у свою кімнату і вирішив продовжити гру. Однак після такої колотнечі він зовсім забув, скільки очок встиг заробити. Тепер він просить Герміону допомогти йому за поточним станом поля гри підрахувати, скільки очок він вже заробив.
Формат введення-виведення:
Програма G2048 зчитує з клавіатури (стандартного пристрою введення) чотири рядки по чотири числа у кожному. Пусті клітинки позначені нулями, непусті можуть містити тільки степені двійки, тобто числа 2, 4, 8, 16, 32, …, 65536 таким чином, що поле в цілому може бути правильною кінцевою або проміжною позицією розглянутої гри.
Програма G2048 виводить на екран (стандартний пристрій виведення) єдине число – шукану кількість очок.
Приклад вхідних та вихідних даних:
|
Введення |
Виведення |
|
0 0 0 4 0 0 0 0 0 2 0 0 0 0 0 2 |
4 |
|
0 0 0 2 2 0 0 0 0 0 2 4 0 2 4 8 |
24 |
Драбина (stairs)
Як відомо, Школа чарування та магії у Хогвардсе має 142 драбини, одина з яких має рівно N сходинок. Саме по цих сходах можна пересуватися, переходячи з однієї сходинки на наступну, перестрибуючи через сходинку або перестрибуючи через дві сходинки, однак перестрибувати через сходинки два рази поспіль не можна. Частина сходинок була зруйнована в одній із сутичок з Волан де Мортом, однак цією драбиною все ще можна користуватися, обов’язково починаючи рух з першої сходинки та закінчуючи на останній.
Альбус Дамблдор не на жарт стурбований станом цих сходів і його цікавить відповідь на таке питання: при зруйнуванні якої максимальної кількості сходинок по сходах все ще можна буде піднятися з першої сходинки на останню.
Формат введення-виведення:
Програма stairs зчитує з клавіатури (стандартного пристрою введення) два цілих числа N та K, загальна кількість сходинок в сходах та кількість зруйнованих сходинок (2 <= N <= 106, 0 <= K <= N-2). Далі зчитуються K цілих чисел, номери зруйнованих сходинок (в діапазоні від 2 до N-2).
Програма stairs виводить на екран (стандартний пристрій виведення) єдине число – максимальну кількість сходинок, які можна зруйнувати, не виводячи сходи з ладу.
Приклад вхідних та вихідних даних:
|
Введення |
Виведення |
|
8 2 6 3 |
2 |
Велика шахова партія (emperor)
Головний ворог Гаррі Поттера лорд Волан-де-Морт, якого багато хто вважав загиблим, таємно повертається у Хогвардс. Для цього він використовує тіло професора захисту від темних мистецтв Квіреуса Квіррела. За його допомогою він починає шукати філософський камінь, думаючи відновити тіло Темного лорда. Гаррі Поттер активно йому протидіє і його друзі – Рон Уізлі та Герміона Грейнджер – допомагають йому в боротьбі. В один з самих критичних моментів Рону пропонується зіграти у чарівні шахи за новими правилами. На шаховому полі крім звичайних фігур знаходиться нова фігура – так званий Імператор.
- На своєму першому ході Імператор збиває любу шахову фігуру, яка стоїть на одній з ним горизонталі або вертикалі та переходить на її місце.
- На будь-якому наступному кроці Імператор збиває будь-яку шахову фігуру на тій самій вертикалі (якщо попередній хід цього Імператора був по горизонталі) або горизонталі (якщо попередній хід був по вертикалі) та переходить на її місце.
- Імператор не може зробити хід, якщо він не може збити шахову фігуру.
Відомо положення шахових фігур на дошці. Рону необхідно терміново розрахувати, яку найменшу кількість Імператорів потрібно поставити на дошку таким чином, щоб вони могли збити усі шахові фігури. При цьому Імператори можуть робити будь-яку кількість ходів, а шахові фігури не рухаються. Розмір дошки: 108 ×108.
Формат введення-виведення:
Програма emperor зчитує з клавіатури (стандартного пристрою введення) ціле число N (1 <= N <= 105) – кількість шахових фігур. Потім зчитується N пар цілих чисел (в діапазоні від 1 до 108), позиції шахових фігур.
Програма emperor виводить на екран (стандартний пристрій виведення) єдине число – найменшу кількість Імператорів для безумовної перемоги.
Приклад вхідних та вихідних даних:
|
Введення |
Виведення |
|
4 1 1 1 2 1 3 1 4 |
2 |
Левітація (levitation)
Як відомо, левітація– це вміння силою думки долати земне тяжіння, простіше кажучи — літати, не маючи крил або інших пристосувань. Змусити літати можна як неживий предмет, так і людину. Левітація вивчається на уроках заклинань в Школі чарівництва та магії у Хогвардсі. На перших з цих уроків учні змушують літати тільки предмети і літають вони в дуже непередбачених напрямках.
Для надання допомоги учням на урок левітації був запрошений відомий усім вчитель фізики Юра Геніальний. Побачивши результати роботи учнів, він жахнувся і попросив Герміону Грейнджер виконати деякі розрахунки, щоб дізнатися, на якій відстані від левітуючого предмету потрібно розміщувати учнів для їх безпеки.
Спочатку він запропонував розглянути матеріальну точку на площині з масою 0.1кг, яка в момент часу t = 0 секунд знаходиться в початку координат та має нульову швидкість. Припустимо, що на точку діють N постійних сил від різних учнів. Для кожної з сил відома пряма її дії, однак напрям сили точно не відомий, тобто сила може діяти вздовж прямої її дії як в одному, так і в іншому напрямку.
Необхідно знайти найменший круг з центром в початку координат, такий, щоб точка в момент часу t = 1 секунд гарантовано знаходиться всередині круга або на його межі.
Формат введення-виведення:
Програма levitation зчитує з клавіатури (стандартного пристрою введення) ціле число N – кількість прямих дії сил (1 <= N <= 105). Потім зчитується N пар цілих чисел (в діапазоні від −103 до 103), які визначають відповідну пряму, що проходить через центр координат та задану точку. Модуль сили, що дії вздовж цієї прямої, визначається довжиною відрізка від початку координат до заданої точки та вимірюється в кг∙м/сек2.
Програма levitation виводить на екран (стандартний пристрій виведення) єдине ціле(!) число – квадрат радіуса круга (в м2).
Приклад вхідних та вихідних даних:
|
Введення |
Виведення |
|
2 1 3 1 -3 |
900 |


