Задача Schoolnet2015d. Лабораторія ІКТ ФМГ17 ініціювала розбудову оптоволоконних каналів зв’язку між школами. На практиці це виглядає так: при наявності коштів між деякими двома школами прокладається оптоволоконний кабель. Робота довготривала, але до початку 3-го туру впорались. Мережні адміністратори навчилися скеровувати пакети між школами будь-яким шляхом, а не лише через прямий зв’язок між ними. Та одразу постало питання підвищення надійності роботи мережі, виключення «мережних колізій». Один із методів, який запропонувала Лабораторія – передача даних деякими лініями лише в одному напрямку. Чим більше таких однонаправлених ліній – тим вища надійність мережі загалом. Яку максимальну кількість каналів можна перевести в режим однонаправленої передачі даних? Звичайно, мережа повинна забезпечувати зв’язок між будь-якою парою шкіл в обох напрямках.
Технічні умови. Програма Schoolnet2015d читає з клавіатури два цілих числа N – кількість шкіл у місті та M – кількість ліній між ними (1≤N≤20000, 1≤M≤200000). Далі читає M рядків, у кожному з яких записано два числа через пропуск – номери шкіл, між якими прокладено лінію. Кожні дві школи з’єднуються не більш ніж однією лінією.
Програма виводить на екран одне число K – максимальну кількість ліній, на яких можна увести односторонній трафік.
Приклад:
|
Введення |
Виведення |
|
5 6 2 1 2 3 2 4 2 5 4 3 4 5 |
5
|
Задача Tri2015. Мешканці далекої планети Трианглії вирішили побудувати новий вівтар у Храмі Священної Трійки. Вівтар повинен мати форму рівностороннього трикутника з довжиною сторони n см, і складеним з камінців у формі рівносторонніх трикутників з стороною 1 см. При цьому n має бути степенем числа три: n = 3k (рис. 1).
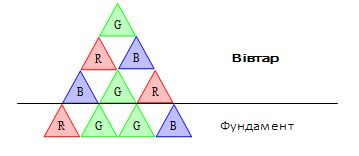
Рис. 1. Приклад вівтаря з довжиною сторони n=3см
Кожен з маленьких трикутників-камінців має бути пофарбованим в один з трьох кольорів: червоний, зелений чи синій. Для того, аби визначити колір кожного каменю майбутнього вівтаря, спочатку створюють допоміжний шар (фундамент) з n+1 каменів, по одному на кожного мешканця. Далі вівтар будується пошарово - спочатку шар над фундаментом, потім другий шар, і так до самої вершини, дотримуючись двох правил:
• якщо кольори двох сусідніх трикутників внизу якогось трикутника різні, то цей трикутник має бути третього кольору;
• якщо колір двох сусідніх трикутників внизу співпадає, то цей же колір повинен мати і поточний трикутник.
Герой Трианглії Тривася Трипупкін спізнився на момент закладки фундаменту. Решта n його друзів вже поклали свої камінці у фундамент, так що там залишилось місце лише для крайнього правого трикутника (синій камінець в фундаменті на рис. 1). Тривася хоче дізнатися, камінець якого кольору він має покласти у фундамент, аби вершина вівтаря була пофарбована в зелений колір.
Технічні умови. Програма Tri2015 читає з пристрою стандартного введення ціле число 1 <= M <= 10 – кількість фундаментів. Далі програма читає з того ж рядка через пропуски М послідовностей символів з множини {r,g,b}, що відображають кольори камінців у майже готовому фундаменті зліва направо (у кожній послідовності символи записані без пропусків, кількість символів у кожній послідовності n = 3k, де k ⩽ 10 , тобто n ⩽ 59049). Програма виводить на пристрій стандартного виведення М підмножин множини {r,g,b}. Кожна підмножина записана в вигляді одного або послідовності символів без пропусків. Послідовності розділено одним пропуском. Якщо Тривася не може отримати зелену вершину жодним з способів, вивести єдиний символ n.
Приклад
Введення 2 rgg ggrggrggr
Виведення: b g
Задача FindLCG Дано 4 цілих невід'ємних числа x0, A, B, k. Вони задають послідовність (лінійний конгруентний генератор) вигляду
xn+1 = (A*xn + B) mod 2k . Треба по заданому цілому невід'ємному числу x знайти його найперший номер в послідовності (мінімальне ціле невід'ємне число n таке, що xn=x).
Технічні умови. Програма читає з пристрою стандартного введення 5 цілих невід'ємних чисел x0, A, B, k, x (1<=k<=64, 0<=x0,A,B,x<2k).
Програма виводить на екран (пристрій стандартного виведення) єдине ціле невід'ємне число - шукане n. Якщо розв'язку не існує - програма виводить -1 .
Приклад
Введення 1 5 7 4 3
Виведення 2
Задача Tram. Керівництво Муніципальної Транспортної Компанії м. Вінниці вирішило встановити нову систему оплати за проїзд у трамваях. Маршрут являє собою відрізок прямої, на якій послідовно розміщені N зупинок. Планується розбити їх на M неперервних зон, що слідують підряд, таким чином, щоб кожна зона містила хоча б одну зупинку. Оплату проїзду від зупинки i до зупинки k необхідно встановити рівною 1+|zi−zk|, де zi і zk ‑ номери зон, яким належать зупинки i та k відповідно.
Відома кількість пасажирів, які відправляються за день з кожної зупинки на кожну іншу. Напишіть програму, що визначає, яку максимальну суму грошей за день можна отримати за новою системою при оптимальному розбитті на зони.
Технічні умови. Програма Tram зчитує зі стандартного пристрою введення N рядків. Перший рядок містить два цілих числа N та M (1≤M≤N≤1000). Другий – одне число, що означає кількість пасажирів, що їдуть від зупинки 1 до зупинки 2. Третя – два числа, що означають кількість пасажирів, що їдуть від зупинки 1 до зупинки 3 та від зупинки 2 до зупинки 3, відповідно. І так далі. В N-ому рядку міститься N−1 число, i-е з них визначає кількість пасажирів від зупинки i до зупинки N. Кількість пасажирів для кожної пари зупинок дано з урахування руху в обидві сторони. Всі числа цілі невід’ємні та не перевищують 10000.
Програма повинна вивести на стандартний пристрій виведення єдине ціле число – шукану максимальну денну суму грошей.
Приклад:
|
Введення |
Виведення |
|
3 2 200 10 20 |
440 |
Задача
Latest10. Вирахувати 5
останніх знаків до десяткової коми і 5 перших знаків після десяткової коми для числа
![]() ,0 ⩽ n ⩽ 100000.
,0 ⩽ n ⩽ 100000.
Технчні умови. Програма Latest10 читає з пристрою стандартного введення число n. Програма виводить на пристрій стандартного виведення 5 останніх знаків до десяткової коми, крапку і 5 перших знаків після десяткової коми без пропусків.
Приклади
Введення: 5
Виведення: 00152.21023
Введення: 7
Виведення: 01136.11266
Завдання підготували Г.Непомнящий, О.Островський, Ю.Пасіхов, Д.Поліщук


